円の中心軸(円の中心を通り,円の面に 垂直な直線)上の点における磁束密度を求めよ。 解 図85に示すように,円の中心を原点Oとして,円の中心軸をz軸とする。円周上 の点Qにある電流素片Ids が,z軸上の点Pにつくる磁束密度は()より dB = µ0 4π Ids×r r3 円と直線の位置関係1: 半径 r r の円の中心と直線 l l の距離を d d とする. これは下図をみれば明らかです. この公式から d d と r r をそれぞれ計算すれば,円と直線の位置関係が調べられます.すなわち,わざわざグラフを書いてみなくても, 代数的な円1の半径 R= 3 , 中心(xc1,yc1) = ( 05, 2) とする。 円2の半径 R= 35 , 中心(xc2,yc2) = ( 2, 6) とする。 、 エクセルを用い円1と円2の交点を求めてみよう。 図3 円と円の交点を求めるエクセルシート

標準 円の接線と作図 なかけんの数学ノート
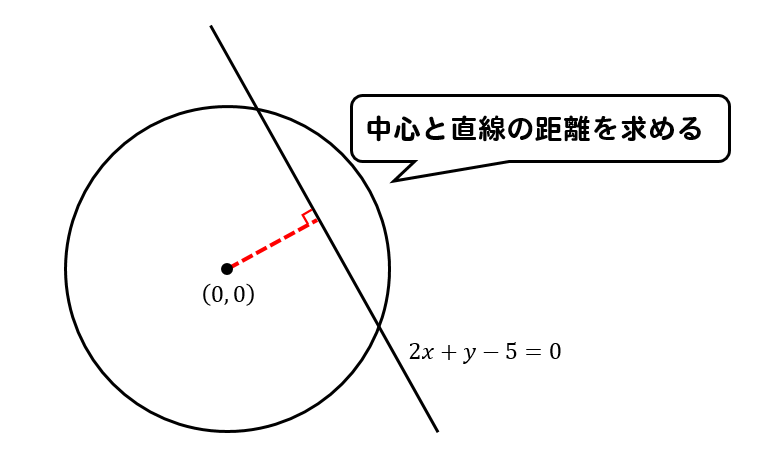
円の中心と直線の距離 求め方
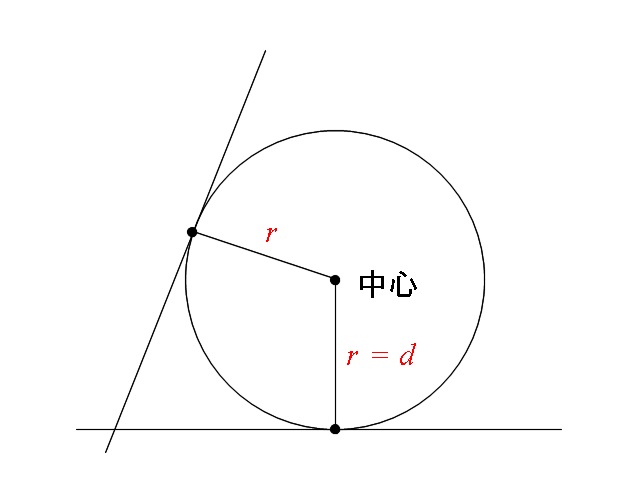
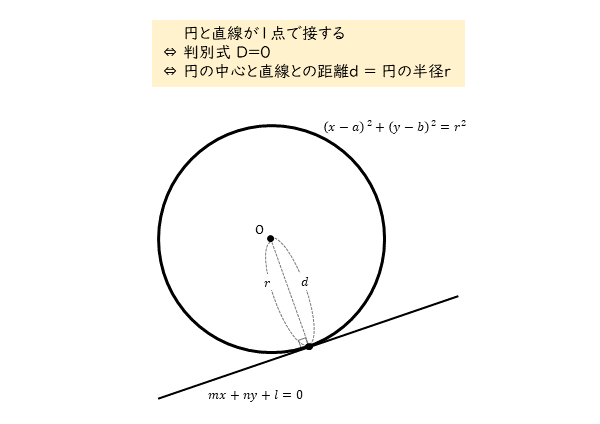
円の中心と直線の距離 求め方- 弧長(円弧の長さ)L、弦長d、矢高(円弧の高さ)h、半径rのどれか2つに値を入力して、残りの2つを0と入力すると(空白にはしないでください)、その残りの2つおよび中心角を計算します。 L=r*θ, d=2*r*sin (θ/2), h=r* (1cos (θ/2))を用い、ニュートン・ラフソン 円の中心と直線との距離が、円の半径と等しいならば、円と直線は接します。 円の中心と直線との距離が、円の半径より短いならば、円と直線は2点で交わります。 実際に図を描いて考えれば、それはそうだなと納得のいくことだと思います。 この考え方を



円と直線の位置関係 大学受験の王道
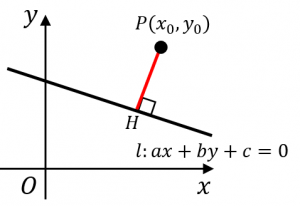
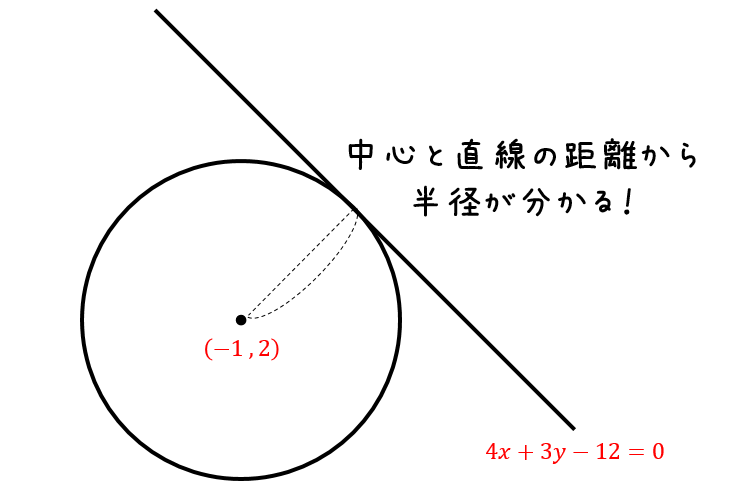
中心と直線の距離: d = a x 0 b y 0 c a 2 b 2 中心と直線の距離についてはここを参照. ホーム>>カテゴリー別分類>>幾何>>円と直線の関係 最終更新日 14年8月15日円と直線に関する入試問題では、2次方程式③を考えるよりも、円の半径rと、円の中心と直線との距離dとの大小関係を考える方がラクに解けることが多い。 例1 円 と直線 の2交点の距離を求める。 解答 円 の中心は ,半径は3 と直線との距離は、110 点と直線の距離 点 P (p,q) と直線 lax by c 0 の距離 d は次の式で求めます. a 2 b 2 ap bq c d (110) 111 点から直線へ下した垂線の足 点 P から直線 l へ下した垂線の足 H は次のように求めます. まず,式(15)から,点 P を通り直線 l に垂直な直線 L
焦点までの距離を固定して、準線を 無限遠直線 (英語版) へ飛ばせば離心率は 0 となり、円錐曲線は円になる。 焦点と準円を用いた定義 編集 任意の円錐曲線は一つの焦点と一つの準円から等距離にある点の軌跡としても記述できる。2点(x1,y1)(x2,y2)を結ぶ直線と 円の中心迄の距離 D は 2点間の距離Hと半径から D=±√(r 2H 2 /4) Xc= (x1x2)/2(y2y1)*D/H;2つの円の半径 r 1, r 2 r_1,r_2 r 1 , r 2 と中心間の距離 d d d について,5パターンそれぞれで以下のような式が成立します。 5つの式を丸暗記するのではなく,以下のように覚えるとよいでしょう。
円弧または円の間の寸法 デフォルトで、距離は円弧や円の中心点まで測定されます。 スマート寸法 ツールで以下を作成できます 円弧または円のエッジ間の寸法。 同心円の間の寸法。 円弧の最小、中心、最大の位置に対する、円弧間や直線との間円の中心と半径を求めるためには、平方完成して式変形する! 円と直線交点の座標の求め方は?計算方法を問題解説! 数学Ⅱ 点と直線の距離公式の覚え方と使い方をイチから解説中心(a,b)で半径r、円周の任意の点を(x i,y i)とすると円は以下の式で表せます。 rと中心とx i,y i 間の距離の差を出す式をとりあえず差を0として作成します。 上記の式を二乗すると 左式を使って上式からカッコを取り除きシンプルにします。




点と直線の距離を求める公式とその証明 数学ii By ふぇるまー マナペディア



1
R :円の半径 k :円中心と垂線への足の距離 R < k の時、直線は円と交わりません。 (直線は円の外にある) √の中が負になると、EXCEL関数 sqrt() はエラーとなる。 垂線の足と交点との距離(S)が求まれば、円と直線の交点座標(x1,y1), (x2,y2)は円の中心の作図方法 まとめ お疲れ様でした! 円の中心の作図は全然難しいものではありませんでしたね。 中心は、円周上のどの点からも等しい距離にある。 垂直二等分線を利用すると、2点から等しい距離にある点が作図できる。円筒面と軸、エッジ、直線、頂点、点、平面との間に距離合致を追加するときも、このオプションを使用できます。 初期状態のデフォルト オプションは 中心から中心(Center to Center) です。 距離配置オプションには次のものがあります。




最後の2円の中心間の距離の求め方が分かりません Clear



数学 B 円と直線の位置関係 北海学園大 久留米大 ページ 2 大学入試数学の考え方と解法
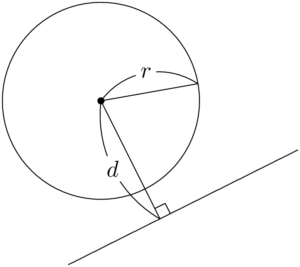
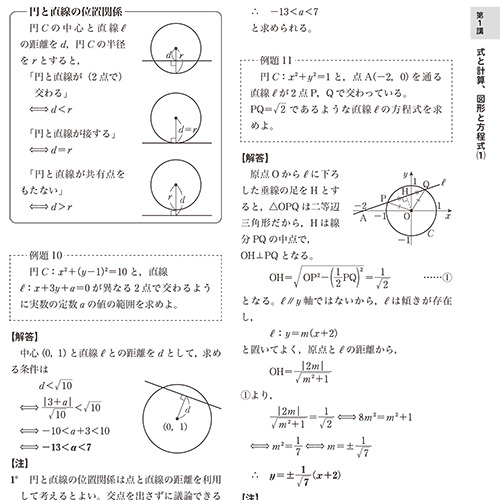
(ⅱ) 円の中心と,直線との距離、 半径 とおいたとき, と の大小関係に着目する。 注)は,『点と直線の距離公式』で求まるね。 d= r= dr d d r d r d r dr (ア)2点で交わる (イ)接する (ウ)離れて点 と直線 の距離は ←分母が間違い! 公式をよく見ると,点の座標 ではなく, の3つある係数の内で, の面目を丸つぶれにして , の2つだけ使うようになっているのです. (具体例とイラストによる解説) 点 と直線 の距離を考えてみます. 直線 上のR1Web Service地図上の距離計測 (円での範囲表示) 住所・キーワードと半径を入力し地図上に 同心円(範囲) を 描画 クリックして計測



Http Www Matsudo Ed Jp Mtd 1 J Index Cfm 1 4067 C Html 4067 Img 0407 0005 Pdf




数学 図形と方程式 中心 直線の距離 と 半径 の関係 オンライン無料塾 ターンナップ
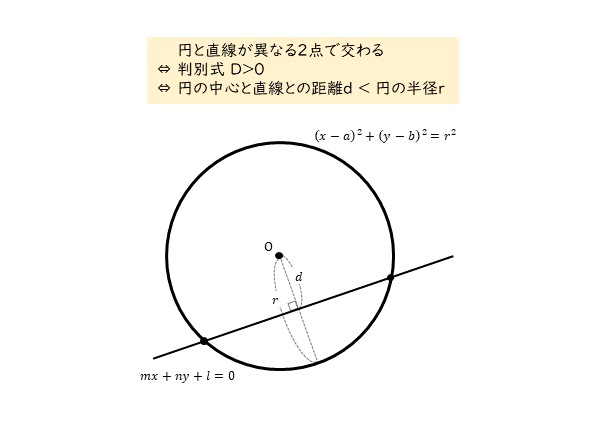
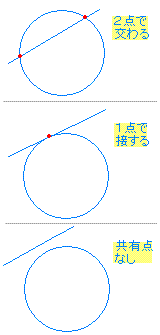
円と直線の方程式が与えられたとき,それらの位置関係を調べるには, (A)判別式Dを用いる方法 (B)円の中心から直線までの距離を円の半径と比較する方法 の2つが考えられる. 円と直線の位置関係 円と直線の位置関係は 異なる2点で交わる 1点で接する 共有点を持たない のいずれか。 円と直線の関係の判定方法 円の中心から直線までの距離と円の半径を比較して判定する。 (点と直線の円の中心は原点で、半径は √2 2 です。 原点と各直線との距離をそれぞれ求め、半径と比べましょう。 (1) は x −y = 0 x − y =



Http Kou Oita Ed Jp Bepputurumigaoka E5 9b E5 81 A8 E6 96 B9 E7 A8 8b E5 8f Ef 95 E6 9c Ef 91 E6 97 A5 Ef E9 87 91 Ef Pdf
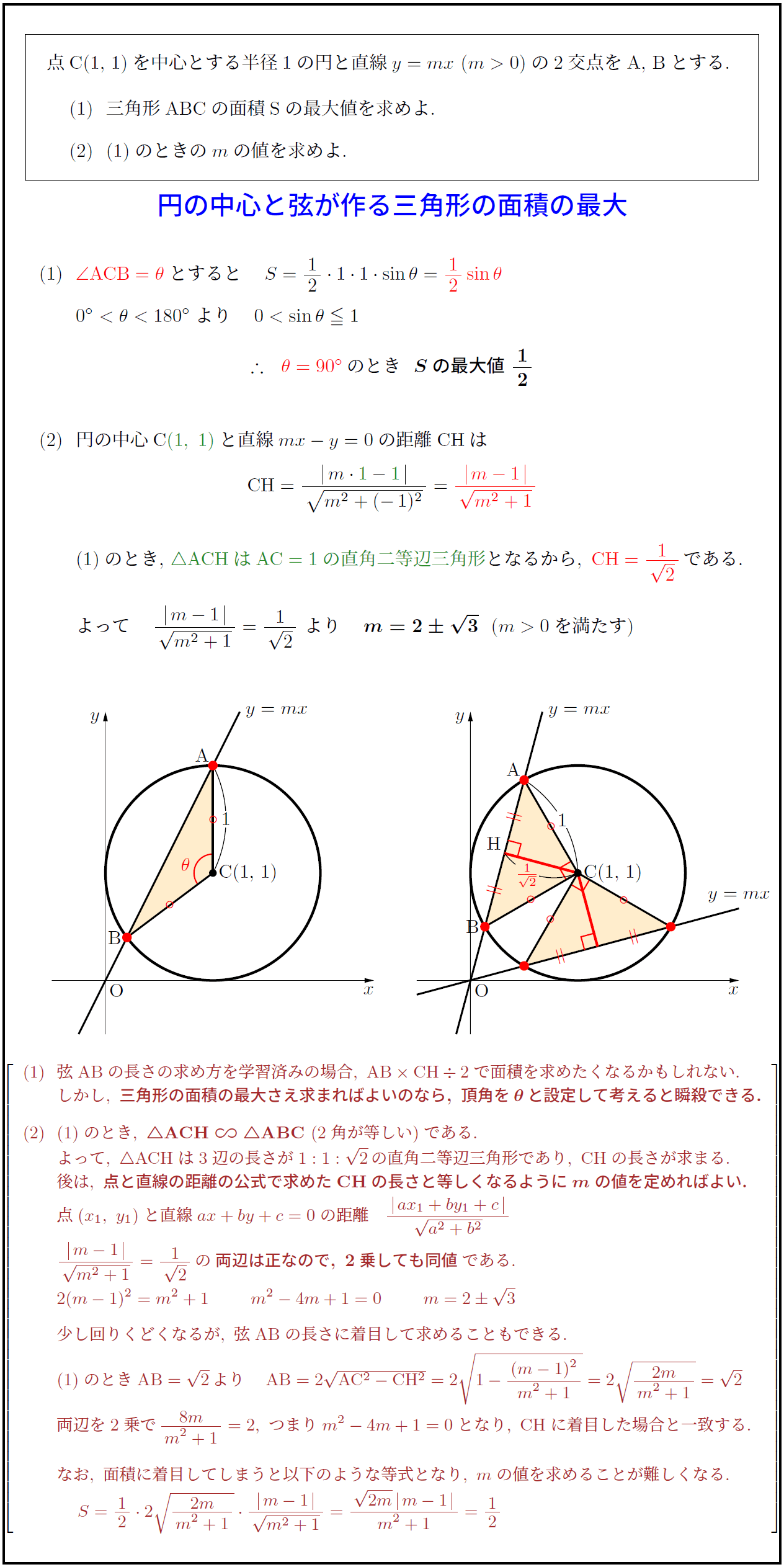



高校数学 円の中心と弦が作る三角形の面積の最大 受験の月
円と直線の共有点間の距離その3 最後に、まったく別のアプローチで解く方法を紹介します。 上の図のように、共有点を A, B とおき、 AB の中点を C とおきます。 このとき、三角形 OAC は直角三角形になります。 OA は半径なので $\sqrt{5}$ です。 また、 OC は点と直線の距離の公式から\ \frac{2点と直線の距離を求める公式 まず「点と直線の距離」ときいて、何を思い浮かべますか? 図のような点Pと直線lの距離を求める方法についてみていきましょう。 図のように、直線l:"ax+by+c=0"上に 半径が r で、円の中心から直線までの距離を d としています。 共有点が2点ある場合、中心から直線に下した垂線の足は、円の内部にあるため、 d < r d < r となります。



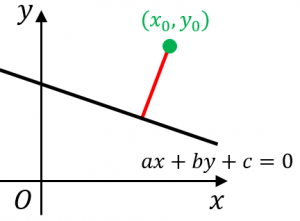
点と直線の距離の公式の意味と中学数学範囲での証明 具体例で学ぶ数学



円と直線の位置関係 思考力を鍛える数学
次の円の中心と直線の距離dを求め、円と直線の位置関係を調べよ。(1)x2乗y 2乗=,x2y10=0で、解答にこれは円の中心は原点であるからと書いてあってなんでこれが円の中心は原点とわかるのですか? ^ は、累乗を表す記号です。 古3点を通る円(Xc,Yc) G=( y2*x1y1*x2 y3*x2y2*x3 y1*x3y3*x1 ) Xc= (x1 2 y1 2)*(y2y3つまり,「外接円の半径は,内接円の半径の2 倍以上である」ことがいえた. ① 傍心と外心の距離 求めた! ,o を abc の外心 i' を傍心 外接 円の半径を r ,傍接円の半径を r' ,傍心と外心の 距離 oi' を, oi' d とおく. becei' を示す 図において,円周角一定




Processing 2点を通る直線と円の交点を求めよう Zawaworks S Diary




無限直線電流線と円リング電流線の間に働く力 特殊相対性理論 電磁気学 数学
円と直線の位置関係 円と直線の方程式を連立してできる2次方程式ax bx c2 0 の 判別式D b ac 2 4 に注目すると,次のようになる。 円が直線から切り取る線分の長さと中点 弦の長さの求め方 ①OM AB なので、中心と直線の距離OM を求める。 ②線分AB の長さは、 OAM図形と方程式:円と直線 円の方程式(直径の両端から求める) 説明 Date年 8月15日 円の方程式は中心 ,半径を とすると, (x−a)2(y−b)2=r2 ( x − a) 2 ( y − b) 2 = r 2 と表すことができました。 このことから,円の中心と半径が導ける条件が与えられて




円の方程式の求め方まとめ パターン別に解説するよ 数スタ



Www Metro Ed Jp Koyamadai H Site Zen Content Pdf
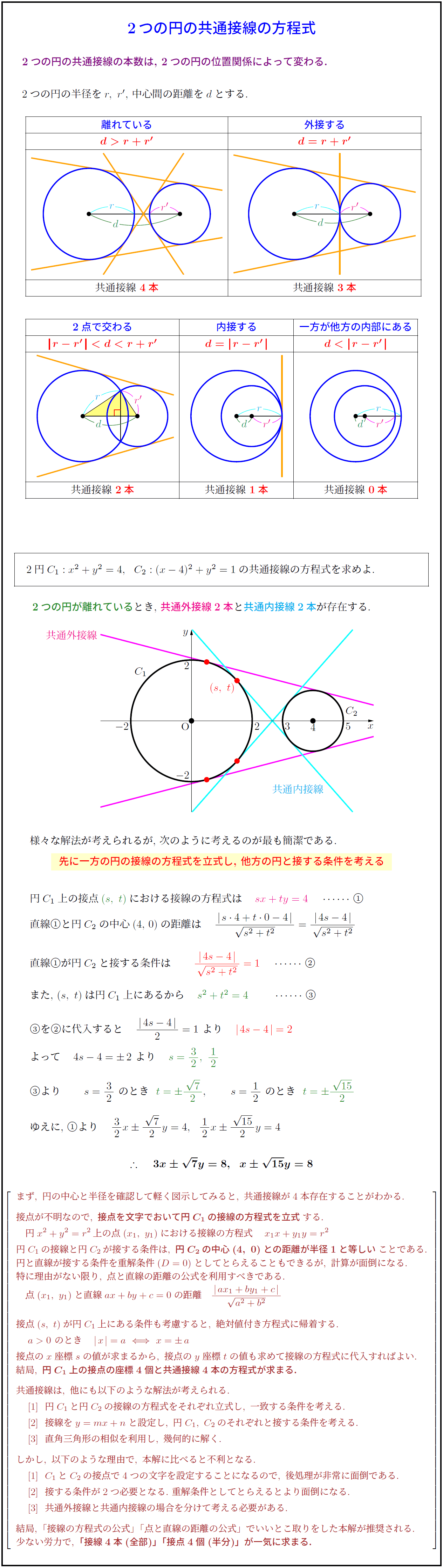



高校数学 2つの円の共通接線の方程式 受験の月



2



点と直線の距離の公式



円の方程式の求め方まとめ パターン別に解説するよ 数スタ
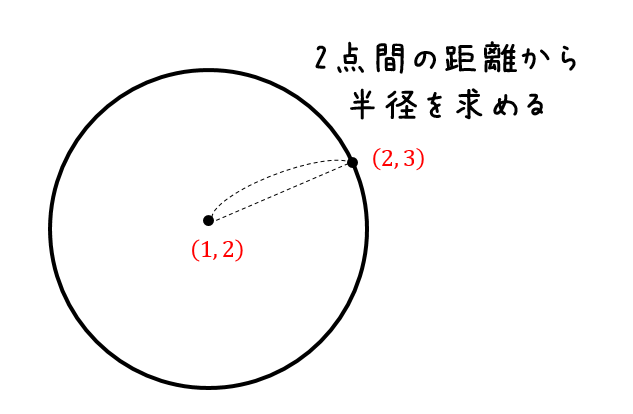



円の方程式の求め方まとめ パターン別に解説するよ 数スタ



Http Izumi Math Jp S Yoshida Matome S2 En Pdf



軌跡とは コトバンク




高校数学 円によって切り取られる線分の長さ 映像授業のtry It トライイット
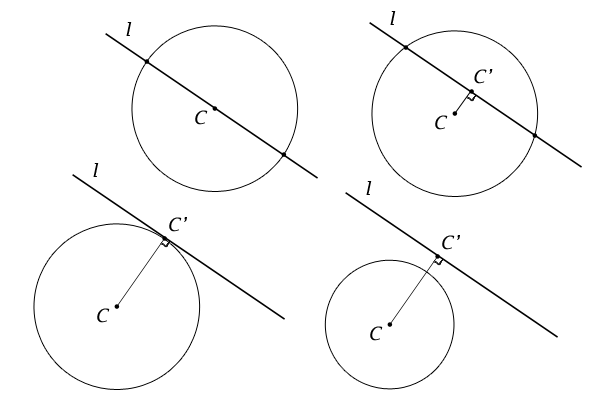



円と直線の距離と位置関係 特に交点 接点 接線について 高校数学マスター



センター数学ii B 練成ユニット1 学研のプライム講座




領域 2 の円の中心と直線l の距離の状態から 答えの最大値7 最小値1 Clear



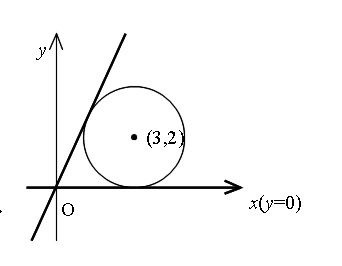
円に接する直線 接線の方程式 の求め方3パターン




図形と式 4 円と直線 その1 東大数学9割のkatsuyaが販売する高校数学の問題集



Googleマップ 地図に距離の円を描く方法 アプリの鎖




点と直線の距離公式の3通りの証明 高校数学の美しい物語



1



2 つの円の位置関係 思考力を鍛える数学




数 B 円の接線は点と直線の距離を用いよう



48s96ub7b0z5f Net En Tyokusen Ten




高校数学 円と直線の位置関係の分類 映像授業のtry It トライイット



点と直線の距離の公式の意味と中学数学範囲での証明 具体例で学ぶ数学




高校2年 数学ii 点と直線の距離 夏季課題 赤城 ᐡᐤᐡ
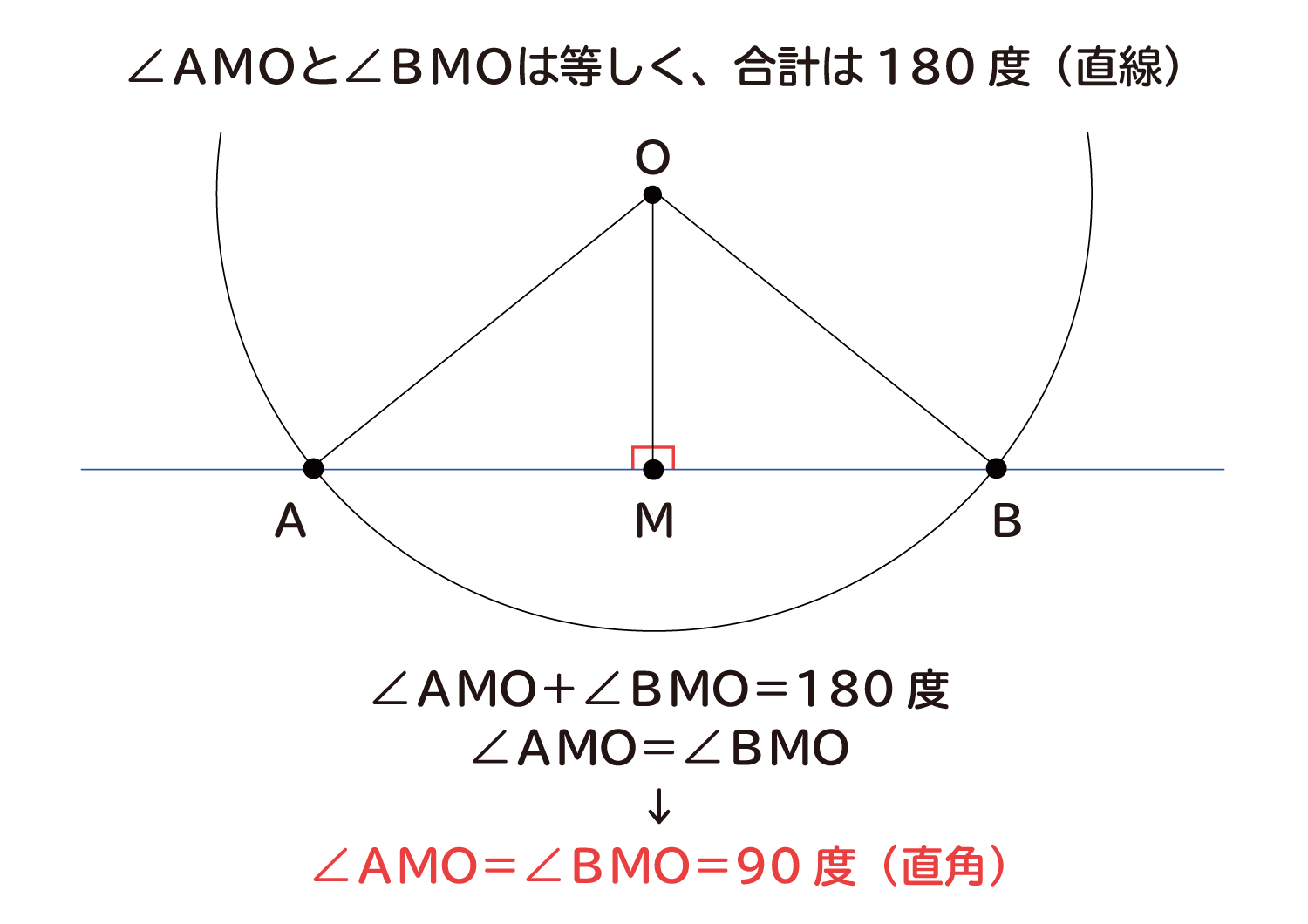



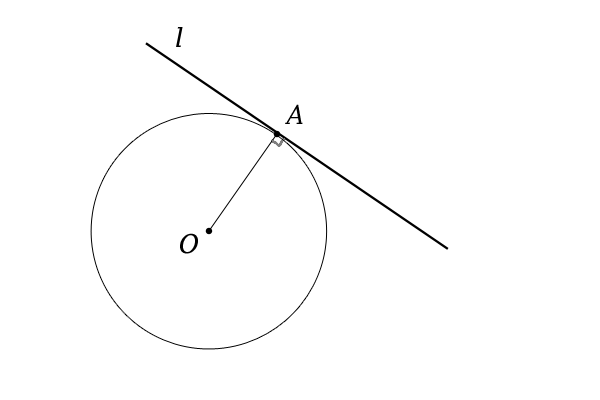
なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル




数 図形と方程式 円の中心 直線の距離 と 半径 の関係 オンライン無料塾 ターンナップ Youtube




中3数学 円の中心と弦との距離 練習編 映像授業のtry It トライイット



円と直線の位置関係 大学受験の王道




円と直線の関係 判別式と点と直線の距離 高校数学の知識庫



Http Www Funairi H Edu City Hiroshima Jp 0423sugaku2nen 3 2 En Pdf




標準 円の接線と作図 なかけんの数学ノート
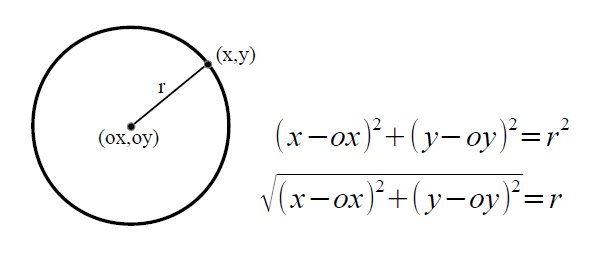



点が円内かを判定 ゆるゆるプログラミング
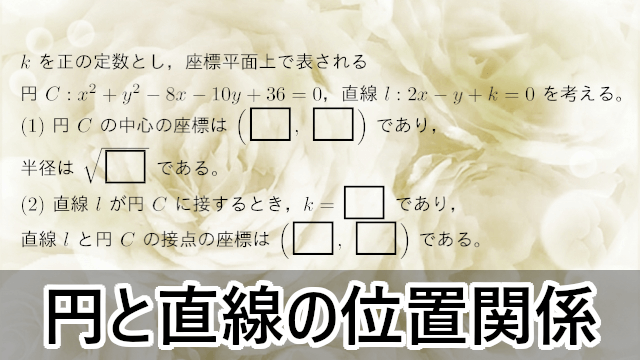



数学 B 円と直線の位置関係 北海学園大 久留米大 ページ 2 大学入試数学の考え方と解法
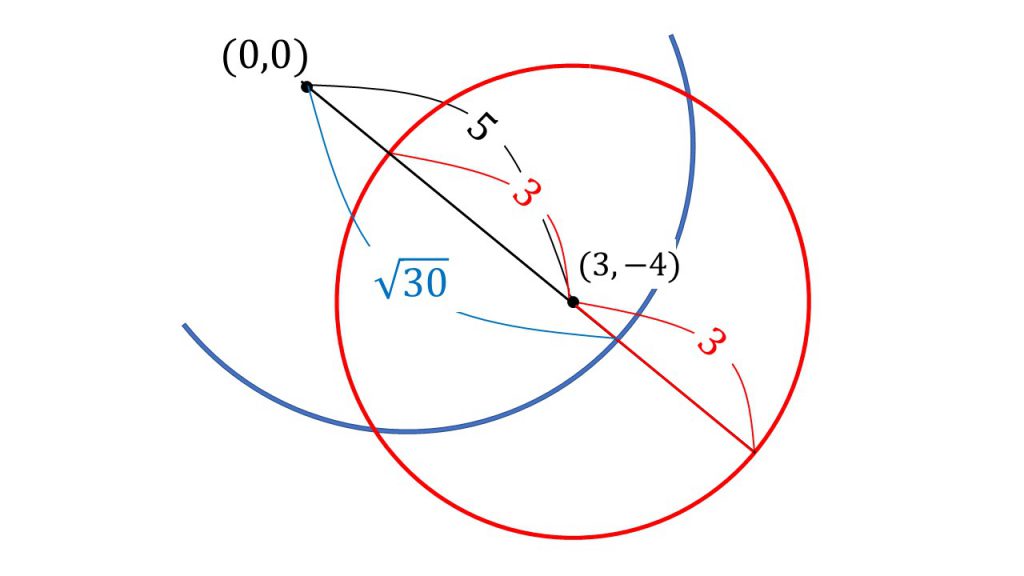



2つの円の位置関係 大学受験の王道



図形と方程式 円と直線の位置関係について 日々是鍛錬 ひびこれたんれん



図形と方程式 円と直線の位置関係について 日々是鍛錬 ひびこれたんれん




高校 数学 図形と式11 点と直線の距離 17分 Youtube



円と直線の位置関係




メルカリ 可 進研ゼミ 高校講座 数学 定着演習6 参考書 600 中古や未使用のフリマ




2つの円の位置関係と円の半径 中心間の距離 高校数学の知識庫



円に接する直線 接線の方程式 の求め方3パターン




数 B 円の接線は点と直線の距離を用いよう 岡山医学科進学塾のブログ
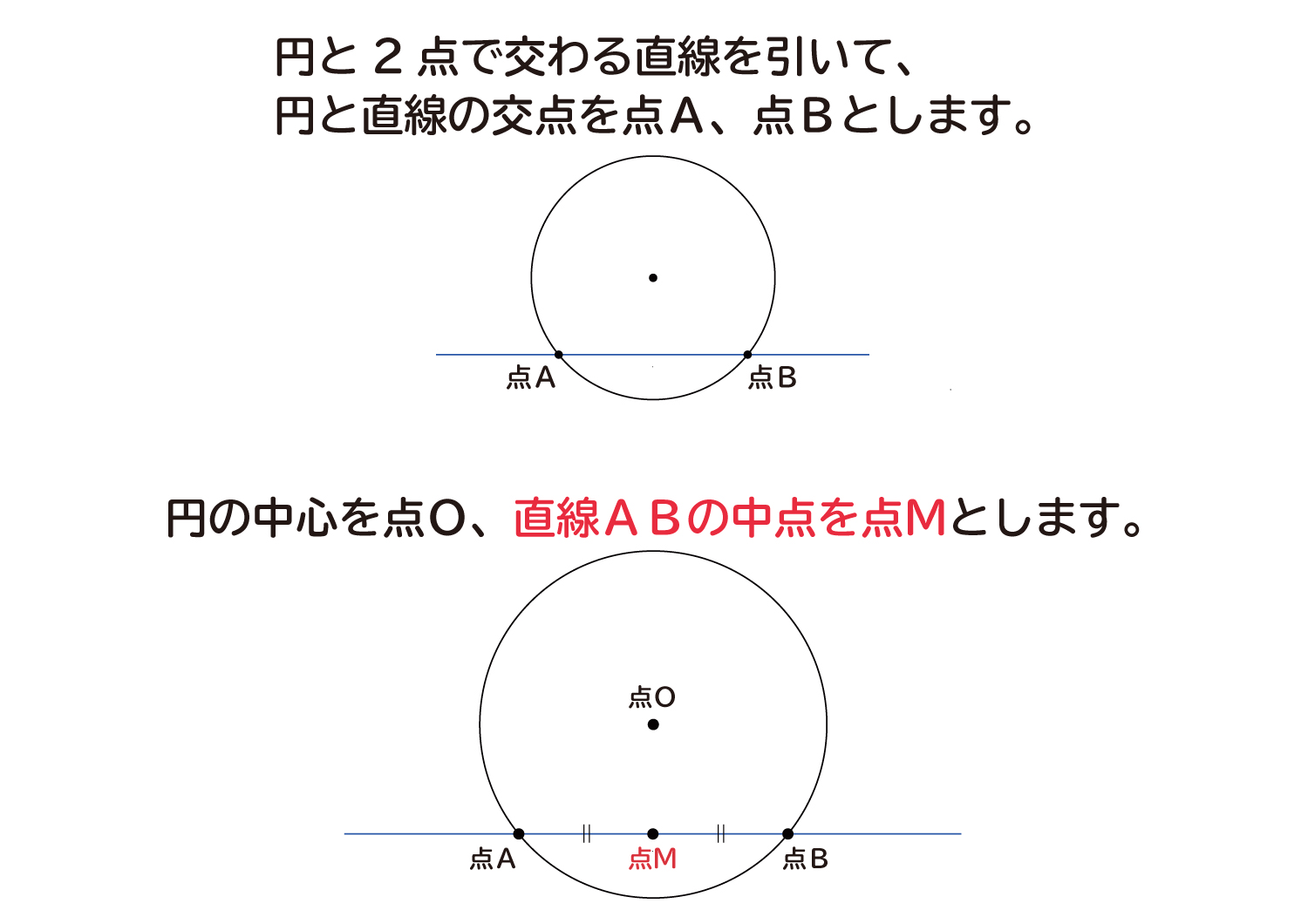



なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル




2つの円の位置関係と円の半径 中心間の距離 高校数学の知識庫



3
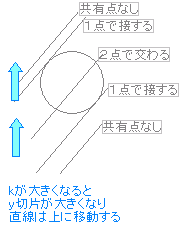



円と直線の位置関係



数 図形と方程式 軌跡と領域 数学用語解説
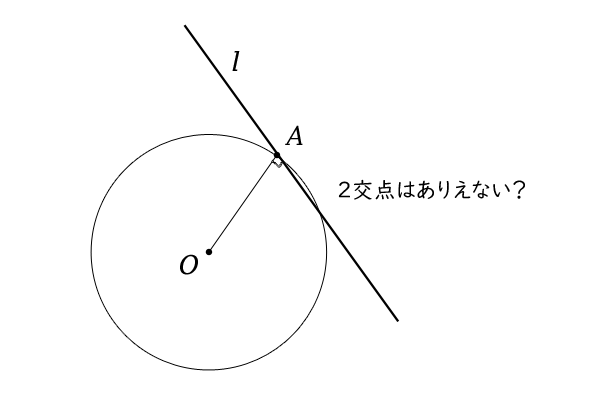



円と直線の距離と位置関係 特に交点 接点 接線について 高校数学マスター




応用 2つの円の交点を通る円や直線 なかけんの数学ノート



Nutsu As 円と直線の交点



Q Tbn And9gcs8govrxmmsri Uq2ku4tuxauhmioafyuowrywnpq8yleyditf9 Usqp Cau
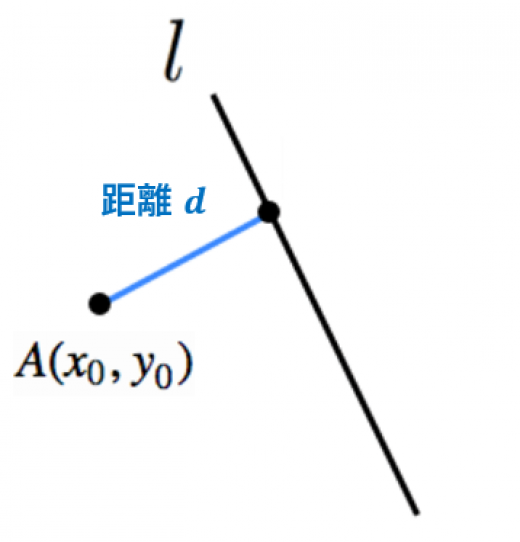



点と直線の距離公式の3通りの証明 高校数学の美しい物語




佐久間 遅ればせながら 点と直線の距離の公式 の導出27通りを全て公開します 高2のときに書いた文章なので稚拙な部分があり 恥ずかしくて晒すのを躊躇っていましたが よく考えたら寧ろ退化していて最近書いた文章の方が稚拙であることに気付いたので




円と直線の交点を求める Qiita




標準 円の接線と作図 なかけんの数学ノート



数 図形と方程式 円の中心 直線の距離 と 半径 の関係 オンライン無料塾 ターンナップ Okedou



円と直線の交点でのコーナr




二円の交点を結ぶ直線からの距離の比 香料ゐっすゐの夢




円と直線の交点を求める Qiita




2円の交点を通る円と直線を一瞬で表す方法とは




数学ii 図形と方程式 6 3 円と直線の位置関係 点と直線の距離 Youtube




円に外接する円の方程式を求める問題 数学ii By ふぇるまー マナペディア
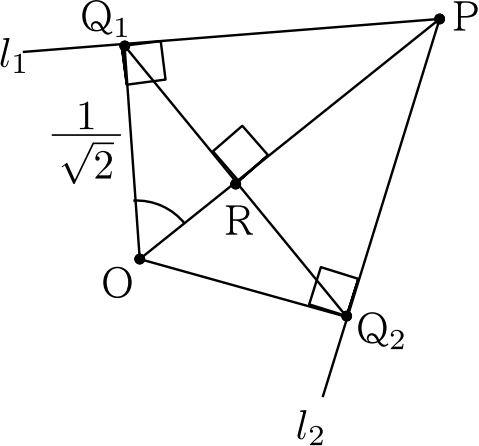



合格る一題 うかる一題 第1問 解答 解説 河合塾マナビス



円と直線 切り取る線分の長さ 弦の長さ を求める問題を解説 数スタ




基本 円と直線の共有点 中心からの距離に注目 なかけんの数学ノート




3分でわかる 点と直線の距離の公式の証明 使い方のコツを分かりやすく 合格サプリ



円と直線の位置関係 思考力を鍛える数学



円と直線の距離と位置関係 特に交点 接点 接線について 高校数学マスター
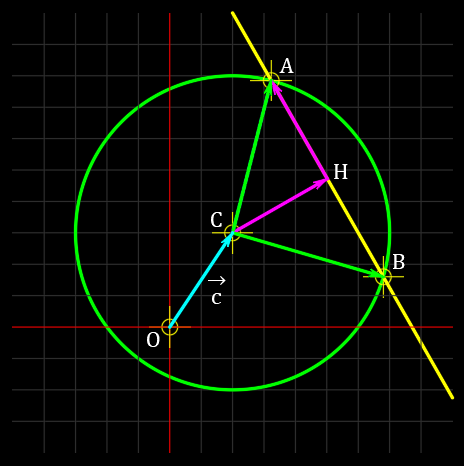



円と直線の交点を求める Qiita



数aの問題です 直線ℓ上に中心があり 2点a Bを通る円の作図方法を教えて Yahoo 知恵袋



円と直線の位置関係 思考力を鍛える数学
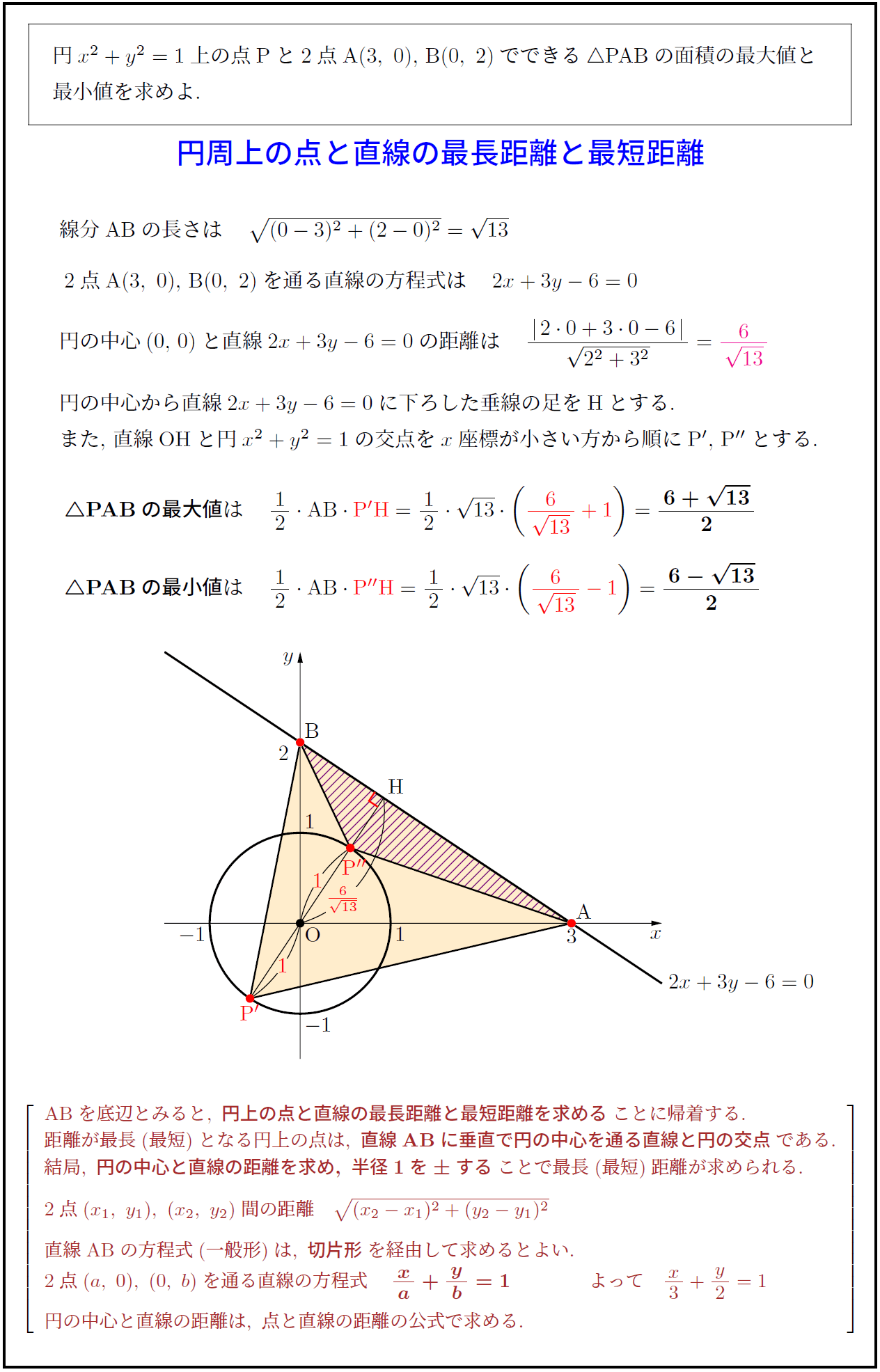



高校数学 円周上の点と直線の最長距離と最短距離 受験の月



3分でわかる 点と直線の距離の公式の証明 使い方のコツを分かりやすく 合格サプリ



円と直線の距離と位置関係 特に交点 接点 接線について 高校数学マスター




高校数学 円と直線の位置関係の分類 練習編 映像授業のtry It トライイット




標準 円と直線の共有点間の距離 なかけんの数学ノート



48s96ub7b0z5f Net En Tyokusen Ten




円と直線の関係 判別式と点と直線の距離 高校数学の知識庫
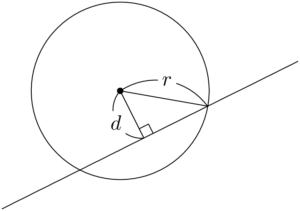



数学 B 円と直線の位置関係 北海学園大 久留米大 ページ 2 大学入試数学の考え方と解法




Standard数学シリーズ ダイジェスト版




高校数学 三角形の内接円の方程式 受験の月



48s96ub7b0z5f Net En Tyokusen Ten




数 B 円の接線は点と直線の距離を用いよう 岡山医学科進学塾のブログ




次の円の中心と直線の距離dを求め 円と直線の位置関係を調べよ 1 X 学校 仕事トーク 教えて Goo




高校数学 円と直線の位置関係の分類 映像授業のtry It トライイット




座標上の 2点間の距離 と 点と直線の距離 の求め方




点と直線の距離を求める公式とその証明 数学ii By ふぇるまー マナペディア




高校数学 円と直線の位置関係 受験の月




円の接線を求める時に 円の中心と直線との距離を使うやり方が一番やりやすいのでしょうか Clear




円の方程式の求め方まとめ パターン別に解説するよ 数スタ




2 と 3 が分かりません Clear




3分でわかる 点と直線の距離の公式の証明 使い方のコツを分かりやすく 合格サプリ



0 件のコメント:
コメントを投稿