A = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) A = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) 弓形 A = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) 円 A = 面積 D = 外径 d = 内径500 日本 円 005 ドル 1000 日本 円 009 ドル 5000 日本 円 046 ドル 日本 円 091 ドル 日本 円 455 ドル 1,000弧長(円弧の長さ)L、弦長d、矢高(円弧の高さ)h、半径rのどれか2つに値を入力して、残りの2つを0と入力すると(空白にはしないでください)、その残りの2つおよび中心角を計算します。 L=r*θ, d=2*r*sin (θ/2), h=r* (1cos (θ/2))を用い、ニュートン・ラフソン法で計算しています。 ※180°以上の中心角の場合、および2つ解がある場合にも対応しました。 動かない
円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく
円 接線 角度 計算
円 接線 角度 計算- https//detailchiebukuroyahoocojp/qa/question_detail/q 0 mon******** mon******** さん 08/1/30 2233 >180°は半分、45°は4分の1ですが、 45°は8分の1ですよ。 円周の角度が360°であるのはご存知ですよね。 円周 (正確には円弧の長さと言います)は角度に比例しますので 角度÷360=円弧の長さ÷円周の長さ となります。扇形の面積と円弧長さを計算 計算する 保存する 復元する 円弧の長さは です。 扇形の面積は です。 円周率πで計算 半径 角度(°)




円周角の定理 角度の計算 中学数学 Youtube
続いてこれらの座標間の角度を上と同じ要領で計算してみましょう。 具体的にはセルに=degrees(atan(d2))と入れればいいです。 こちらもenterにて確定、オートフィルで処理します。 最後にこれらの角度の差をとれば、3点の座標から角度を計算することができます。そして、この角度はrad(ラジアン)という単位で表す。このとき、半径r、中心角θradに対する弧の長さはrθとなる。 360°法との関係は、半径1の円の円周が2πで、その中心角が2π(rad)なので 360°= 2πrad 180°= π rad 90°=1/2πrad 60°=1/3πrad 45°=1/4πradP点から円の中心への角度(α)は tan(α) = ( ycyp ) / ( xc xp) となる。 逆関数を使い、αを求める。 α = tan1(( ycyp ) / ( xc xp) ) エクセルの関数は =ATAN2( xcxp , ycyp ) となる。 P点、接点S1、円中心の角度は直角である。 よって、円中心、P点、接点S1の角度θは簡単に求まる。 sin(θ) = R(円半径)/L(P点から円の中心までの距離) sinの逆関数を使用し、
立体角の計算例 円錐の立体角は、 2 π ( 1 − cos θ 0) という公式で計算することができます。 ただし、 θ 0 は円錐の中心軸と母線がなす角度(平面角)です。 円錐の底面を円板をみなせば、「円板が張る立体角の公式」と言うこともできます。幾何学的定義:A ・ B ≡ A * B * cosθ A × B ≡ A * B * sinθ代数的定義 :A ・ B ≡ Ax* Bx Ay* ByA × B ≡ Ax* By Ay* Bx なので,両者を併用すると簡単に角度および回転方向 (180°< θ ≦ 180°) が求まる. C/C の場合は atan2(y, x) 関数,C# の場合はMathAtan2(y, x) を使うと, θ = atan2(A×B,A・B) (単位はラジアン,引数の順序にも注意) パーセントを円グラフにするにはどんな計算をすればいいんでしょうか?円全体の角度 360° が 100% に対応するように、各成分・内訳の%に応じた角度を求めて行けばよい。時計の文字板でいえば、 1時あたり 30° = % 3時、6時、9時が
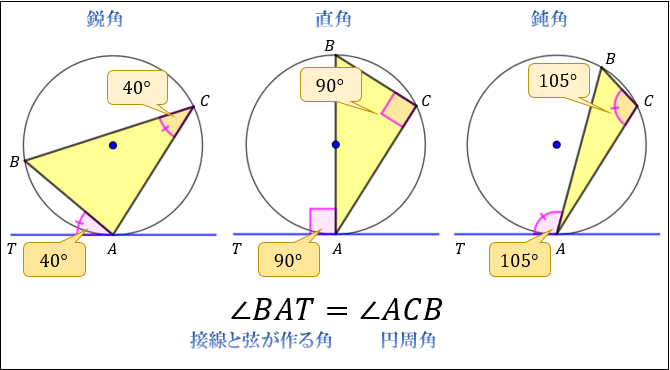
下図のように、中心oを通る直線と円との交点をdとします。 円に内接する四角形の対角の和は180°なので ・・・① となります。また1で証明した接弦定理を使うと ・・・② となり、直進の角度は180°なので ・・・③ となります。①、②、③を足せば円1の半径 R= 25 , 中心(xc1,yc1) = ( 05, 2) とする。 円2の半径 R= 15 , 中心(xc2,yc2) = ( 3, 7) とする。 、 エクセルを用い円1と円2の共通接線を求めてみよう。 図3 円と円の共通接線とそのグラフ うまく接線が求まりました。円角度座標計算, 単曲線(要素計算)(Web 測量計算) お手軽に測量計算(単曲線(要素計算))ができる Webページです。 半径と交角を入力し、他の要素(接線長,曲線長,外線長,中央縦距,弦長)を計算




三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ




円 扇形 の面積 周や弧の長さの公式 数学fun
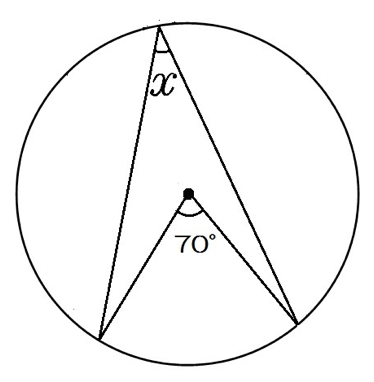
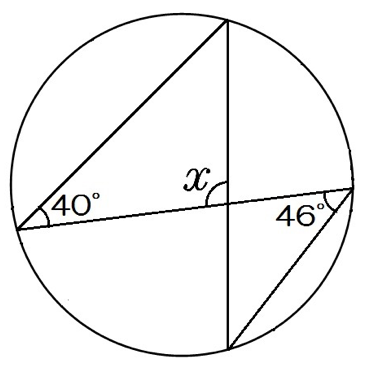
どういうものだったかというと、まず座標平面上で半径が 1 の円である単位円を考えます。 この円上の点を一つとって原点と結びます。 この時 \(x\) 軸から測った角度(動径のところでやりましたね)を \(\theta\) とするとこの点の座標がまさしく角度 \(\theta\) の \(\cos\) 、\(\sin\) だったので消失点の角度計算 2点透視で視心 (VC)から2つの消失点 (VP1,VP2)までの距離a,bが判明している場合に、VCSP間の距離(=90°視円錐の半径)とSPから見た各消失点の角度を算出します。 3点透視の場合でも使えますが、VCを0°消失点に読み替えてください。 長さd,e円周角は中心角の半分 同じ弧に対する、 円周角は中心角の半分 だよ。 すると、図の角度が分かるね。 ここから、三角形の 外角の定理 を使うと、 ∠x+50°=100° となるよ。 ちなみに、この三角形の 2辺は円の半径 でできている、つまり 二等辺三角形 になっていることから、答えを求めることもできるよ。 (1)の答え




円の弧長 弦長 矢高 半径のどれか2つを与えて残りを計算 高精度計算サイト



東大入試の有名問題 から円周率を探求する とてつもない数学 ダイヤモンド オンライン
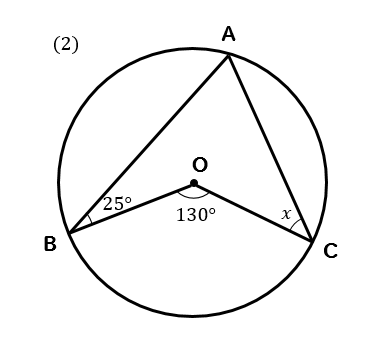
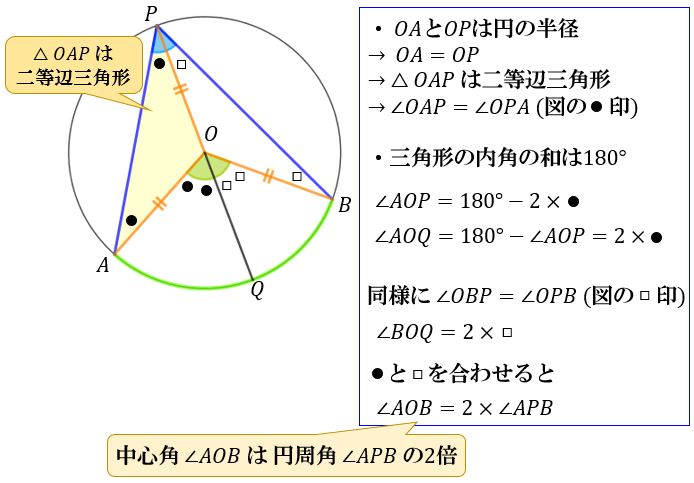
データムを必要とする幾何公差その2~姿勢公差の直角度~:産機設計者が解説「公差計算・公差解析」(9) (1/4 ページ) データムを必要 角B=180°-(30°+45°) =180°-75° =105° と計算できます。 この角Aように、あらかじめわかる角度を図に記入して、三角形の内角と外角の関係(三角の旗)を利用すると簡単に正解が得られる問題はたくさんあります。 答え 角A=1°、角B=105°一つの弧に対する「円周角」の大きさは,「中心角」の半分になります. OC=OB= (半径)だから OBCは二等辺三角形になる. 二等辺三角形の2つの底角は等しいから ∠ B=∠ C (1) ∠ BOA=∠ B∠ C (2) 差で示します. 中心角92°が書いてあって,円周角が



円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ




中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生
となり、角度で考えれば1″以下の誤差となるため、偏角設置において問題はない。 3. 偏角の計算方法 偏角の計算方法は、次のように行えばよい。 ① 中心杭設置計算に必要な接線長(tl:bc~ip間)と曲線長(cl)を計算する。これを右クリックするとこの円が表示されます。私が望むのは、クリックイベントが発生したときに各パイの角度を計算することです。私は public void mouseClicked(MouseEvent e) { PointerInfo a = MouseInfogetPointerInfo();初心者のためのFlashレベルアップ講座 三角関数を使った円運動 (三角関数、角度とラジアン) 概要 青ボールを好きな位置にドラッグしてみてください。 それに合わせて角度、ラジアンの数値が変化します。 本来FLASHの座標は左上が原点の0,0ですが




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット



プチコン講座 角度計算の基本 ラジアン 三角関数
傾斜角度の計算 角度への換算は、arctan(勾配)を用いることで行うことができる。 また、arctanで求めた結果はラジアンで出てくるので 角度(°) = arctan(勾配) × 360 ÷ π で計算することができる。 距離の計算 三平方の定理より 斜辺 2 = 水平距離 2 + 高さ 2Point d = agetLocation();中心角の半分が必ず円周角になる 円周角の定理では中心角が頻繁に利用されます。 この理由として、円周角と中心角は以下の関係があるからです。 円周角 × 2 = 中心角 例えば円周角が30°の場合、中心角は必ず60°です。 円周角を二倍すれば中心角の角度になります。 一方で中心角が80°の場合、円周角は必ず40°です。 中心角の半分が円周角の角度です。




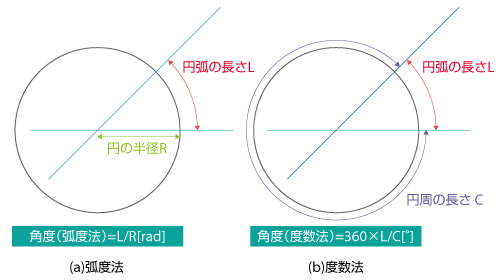
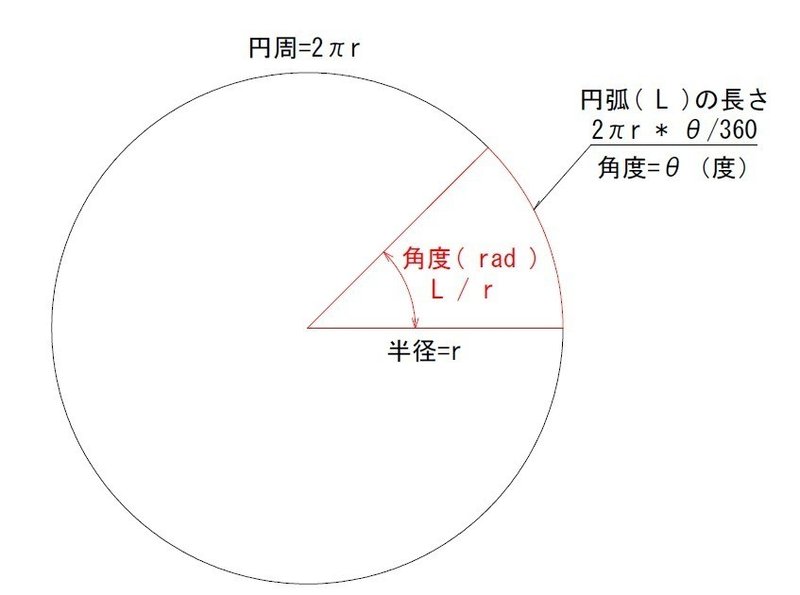
ラジアン 弧度法 の意味と 度 への変換方法




円の中心からの角度から真円の円周上の座標を計算する Youtube
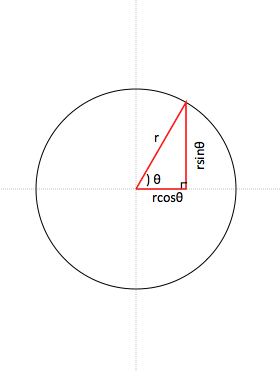
角度を調べる・小学生算数ドリルのページへようこそ 上記のボタンから角度を調べる・小学生算数ドリル (PDFプリント)がダウンロードできます。 個人利用は無料です (家庭以外での配布は有料です)。 スマートフォンやタブレットなどからも印刷できる角度の計算はどうしても小数の計算になるから、計算ミスをしやすいからね。 円を書く コンパスで作りたい大きさの円を書こう。 円グラフを書くときには円の中心が必要だから、コンパスを使うといいんだ。コンパスなら、はりあなが円の中心になるよ。 三角関数で角度から座標を定めるふたつの方程式 まずは、ふたつの方程式を以下に示しましょう。 第1は、原点 ( 0, 0) からの距離 r と x 軸正方向となす角度 θ から座標 ( x, y) を求めます。 x = r cos θ y = r sin θ 第2は、座標 ( x, y) を原点 ( 0, 0) から




円周角の定理 円周角と中心角の関係は中学や高校でよく出るぞ 中学や高校の数学の計算問題



測点の角度 数学 パースフリークス
基本的に、三角関数の角度は 半径 \(1\) の「単位円」 を利用して求めることができます。 単位円 \(1\) 周分の角度は、度数なら \(\color{red}{360^\circ}\)、ラジアンなら \(\color{red}{2\pi}\)下の図のように円周上に15個の任意の点AからOをとり、1つおきに直線で結びました。角AからOまで15個の角の和は何度ですか。 → 解答 平面図形の角度の発展問題 問題1 解答 問題2 90deg === 05radian 180deg === 1radian 270deg === 15radian 360deg === 2radian 半径r = 1 を基準にした時の円の 円周 の長さと角度を関連づけている 別の言い方をすると 円周の長さを 2つのr で切り取った長さを rの長さとの比率で表すもの 円周は 直径2r * π なので,ラジアンの基準になる円の円周は 2πとなる 360degの時の円周 === 2π === 360degの時のradian 2π/r === 2π



円と三角形 角度 中学から数学だいすき



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ
この公式の意味は、円の面積に「360° に対する中心角の割合をかける」ことになります。 「半径が等しい扇形の弧の長さは、中心角に比例する」ということがポイントです。 いま、半径 r の円を考えると、この円周は 2πr ですね。中心角は 360° です。直径の円周角は、つねに90° 40°という角度がヒントになっているけれど、同じ弧に対する円周角や中心角も見当たらないし、使いづらく感じてしまうね。 そこで、 ∠xの方を動かす ことを考えよう。 これは、 同じ弧に対する円周角 が存在するよ。 答えが見えてきたかな? 直径の円周角は、つねに90° 。 つまり、∠x+40°=90° だよ。 (2)の答え この角度θをエクセルで求める方法です。 実際にマーケティングの分野でも角度を求めることができれば、 原点からの距離と角度で順位付けできたりする ので、便利になりますよ! 実際に、座標からの角度計算を活用するマーケティング関連記事もチェック!




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




勉強しよう数学 ベクトルによる円周角の定理の確認



円の中心からの角度から真円の円周上の座標を計算する Gamesprit




中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット



1
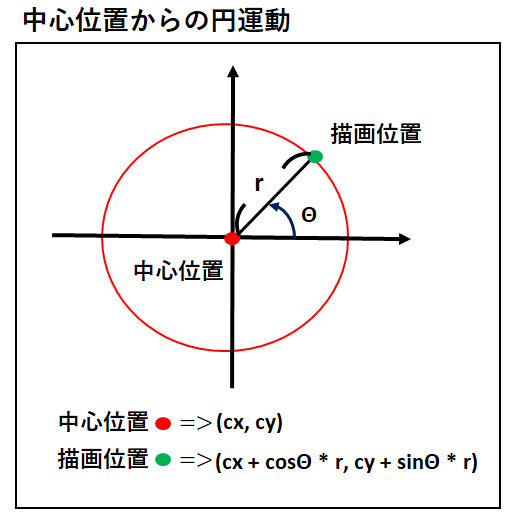



ゲーム 円運動
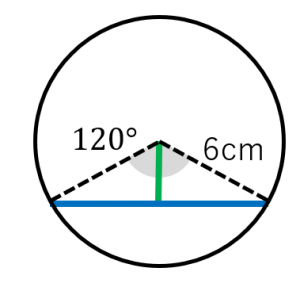



弧の長さと弦の長さの求め方 円周角との関係など 具体例で学ぶ数学
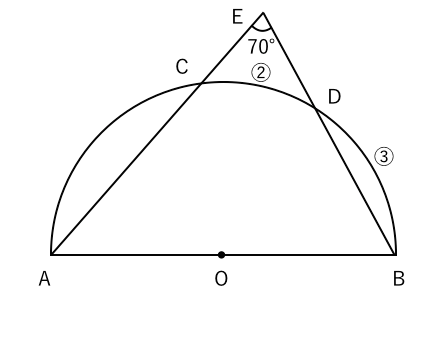



円周角と比の問題 苦手な数学を簡単に




中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット



円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく



角度と長さを自動計算のスクリーンショット 2枚目 Iphoneアプリ Appliv



円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ



三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ
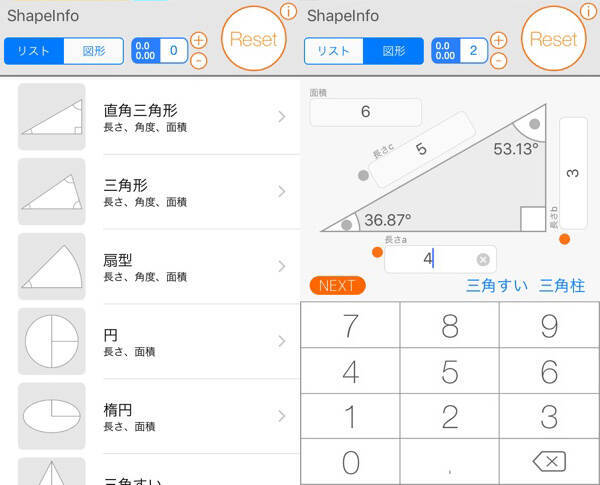



三角形や球も 様々な図形の面積や角度がすぐに分かる 図形電卓 が超便利 16年2月5日 エキサイトニュース




08 号 回転体の芯ずれ算出方法及び芯ずれ算出システム Astamuse




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ
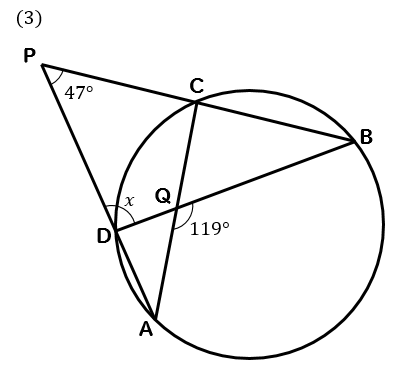



円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ




曲線計算 ダイアログ ボックス Civil 3d 16 Autodesk Knowledge Network




円周角の定理 角度の計算方法と中心角 弧の長さの関係 リョースケ大学




円周角の定理 角度の計算方法と中心角 弧の長さの関係 リョースケ大学




円周角の定理 角度の計算 中学数学 Youtube
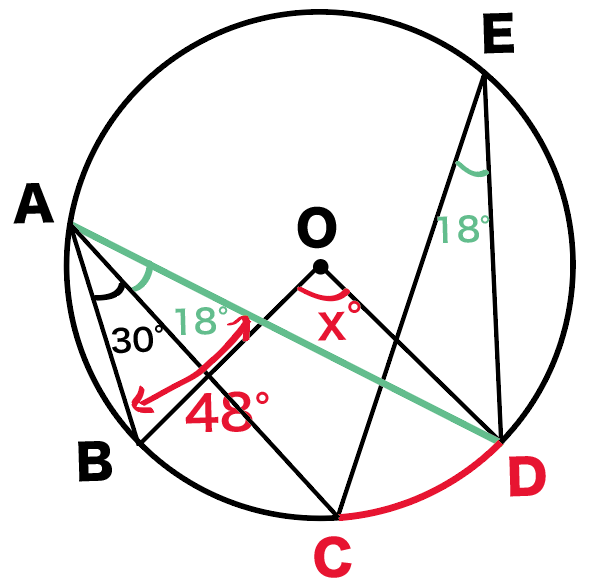



円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく
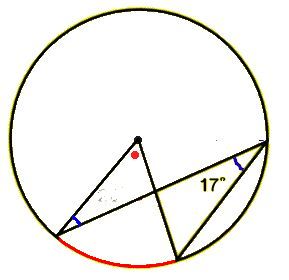



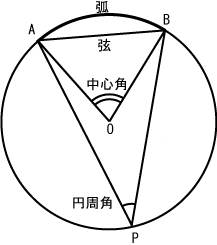
円周角と中心角



代表長さの選び方 3 角度 投稿一覧




高校数学a 共円条件 4点が同一円周上にある条件 受験の月
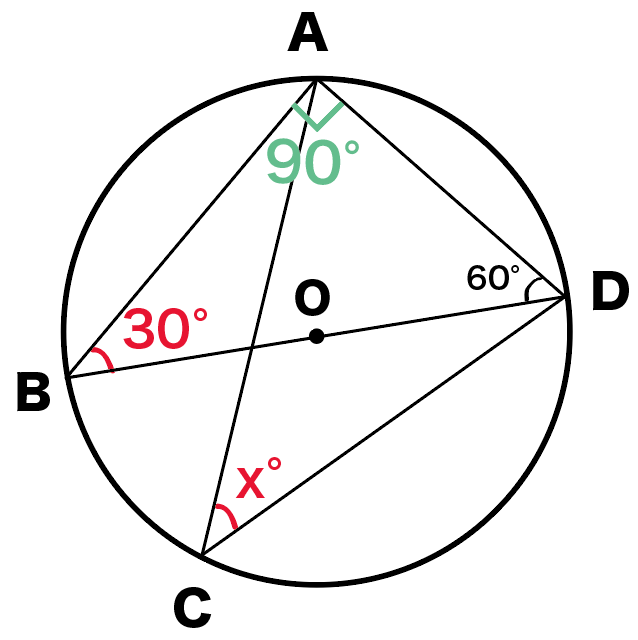



円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく




6本の缶を最短の紐で束ねる意外な方法とは 円と球の不思議な雑学 横山 明日希 ブルーバックス 講談社 1 4



円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく



1



1




O 55 Descubre Como Resolverlo En Qanda



測量士補資格試験 度分秒からラジアンへの変換 八重樫剛 Note




レールの曲率からfredoscale Radial Bendingで曲げる角度を計算する方法 ドナドナされるプログラマのメモ




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




円の中に三角形角度の求め方 いろんな角度の三角関數を単位円で考える Qmog Fi




円周角の定理 角度の計算方法と中心角 弧の長さの関係 リョースケ大学



1




接弦定理とは何か 角度別に分かるその証明方法 アタリマエ



曲線設置の計算2 日曜土木検史郎参上




円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ



角度の呼び方 度 分 秒 の変換 計算式



三角関数の角度は 3分でわかる求め方 公式と計算 表との関係




勉強しよう数学解答集 円の一部分で円周角が一定になることの計算での確認
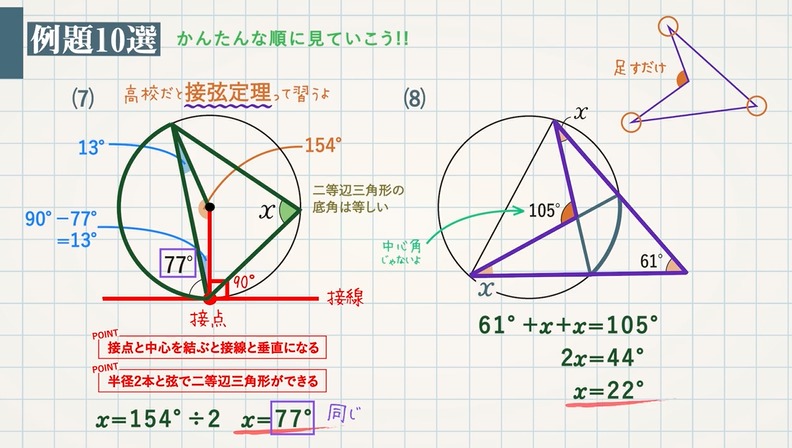



円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者




角度の計算 裏技まとめ 教遊者



角度 Wikiwand




円周角の定理の計算1
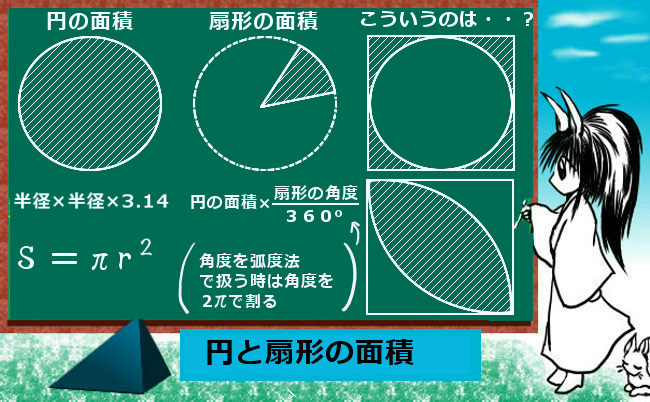



円 扇形に関連する面積の計算 理数系無料オンライン学習 Kori
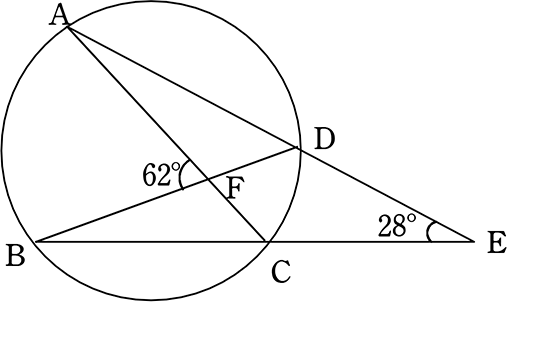



中学数学 円周角 中心角




円周角の定理の基本 計算 無料で使える中学学習プリント




円の中心からの角度から真円の円周上の座標を計算する Gamesprit
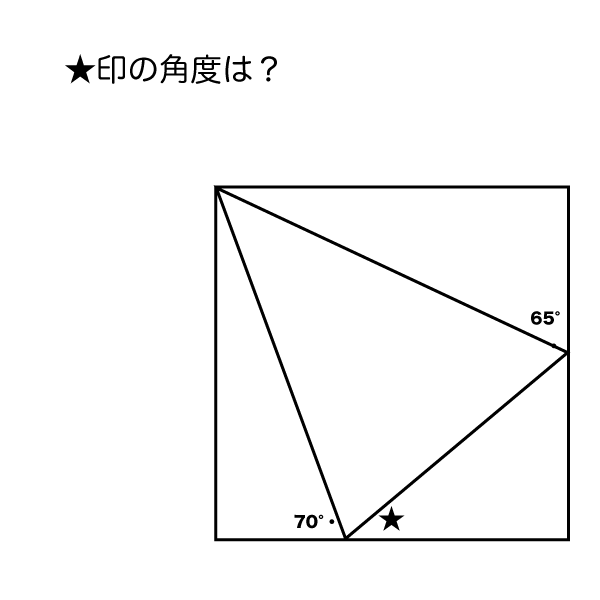



合同条件で解く角度計算 受験算数入門




円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典
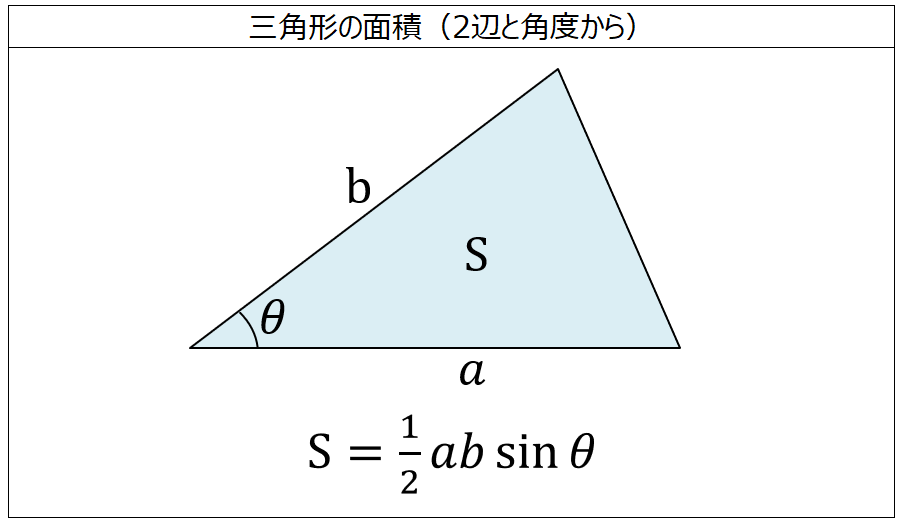



面積の計算 三角形 2辺と角度から 製品設計知識



円と三角形 角度 中学から数学だいすき




円周の公式 なぜ直径 円周率で計算できるのか 円周率を調べる方法 数学fun




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




全円分度器 おけら書房 旧 ラスカル先生




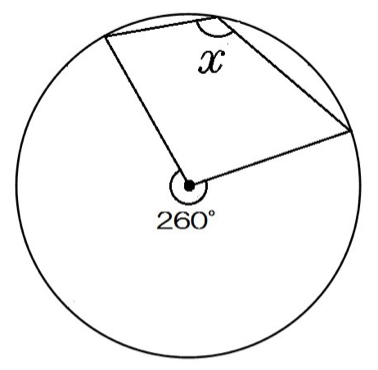
360 をまたぐ角度の計算方法 Autodesk Community International Forums




小4算数 角度を計算で求められるの Youtube




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者



円の接線と角度 中学から数学だいすき




Takawo Shunsuke على تويتر 画面上に複数の円をランダムな位置に配置する 各円の円周上の点の距離を計算 し 一定以下の場合に2点間に線を引く 線の色を距離や角度で周期的に変化させる T Co Xpxwlmeos4 P5js Creativecoding Dailycoding T Co



マシニングで真円の円周上の座標を円の中心からの角度計算はどうすれば良い Yahoo 知恵袋
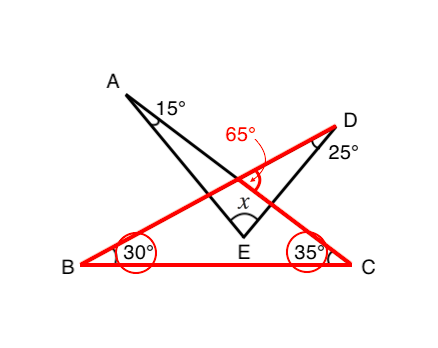



角度を求める問題 スリッパを探そう 苦手な数学を簡単に
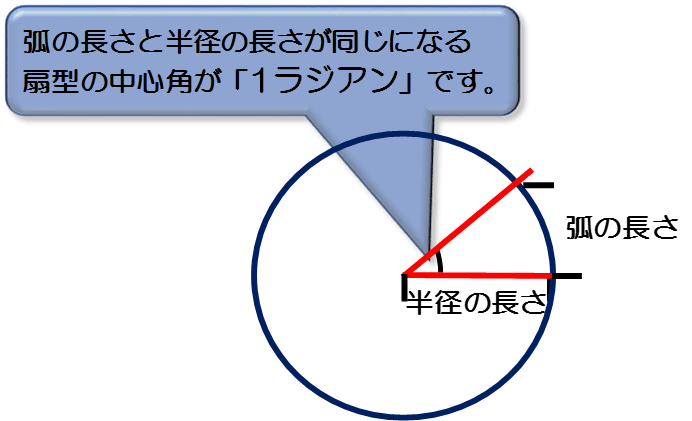



Vba 三角比をもとめる Sin関数 Cos関数 Tan関数 角度をもとめる Atn関数




面白い数学の問題 角度を計算しよう 小学生の問題集より そらの暇つぶしch



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典



角度の計算 裏技まとめ 教遊者




Amazon Co Jp 壁掛け時計単位円数学教師壁掛け時計三角法前計算教室の装飾幾何学ラジアンラベル付き角度値壁掛け時計 ホーム キッチン



中学数学 円周角 中心角




円周角の定理 角度の計算方法と中心角 弧の長さの関係 リョースケ大学
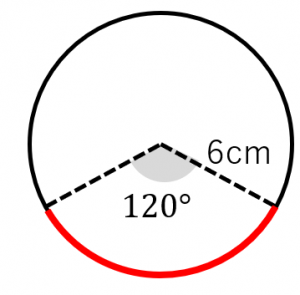



弧の長さと弦の長さの求め方 円周角との関係など 具体例で学ぶ数学




数学 中3 57 円周角の定理 少し応用編 Youtube
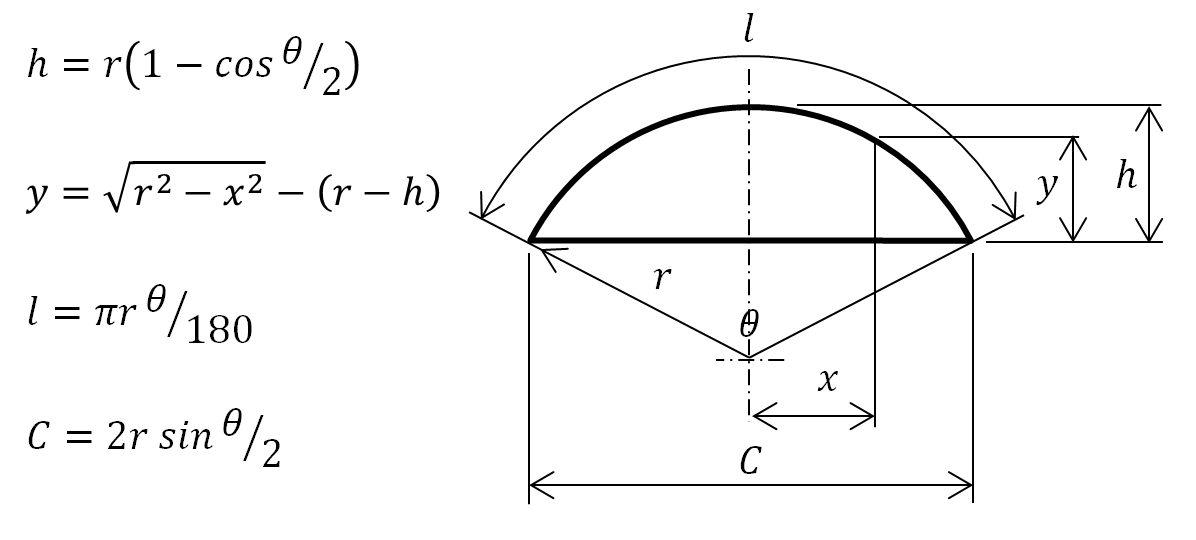



円弧高さ 円弧長さ 円弧長さ 円弧幅の計算 1 高精度計算サイト




円の周りの長さを計算しよう 家庭学習レシピ




円周角の定理 角度の計算方法と中心角 弧の長さの関係 リョースケ大学




扇形の弧の長さの求め方 公式と計算例




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者




三角形の辺の角度を調べる方法 数学 21



円周率を疑ってみた Officeの魔法使い




円の中心からの角度から真円の円周上の座標を計算 座標早見表 Gamesprit




図形計算機 En App Store




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




楕円の円弧の話 カシオの高精度計算サイトkeisan Casio Jpに 楕円の円弧 弦長 矢高を長軸半径 短軸半径 中心角から求める をup Fallen Physicist Rising Engineer



0 件のコメント:
コメントを投稿