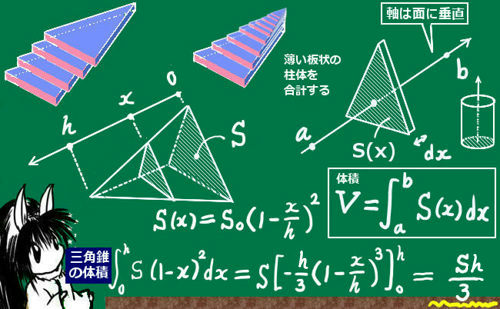
具体例で学ぶ数学 > 図形 > 円柱の表面積と体積を求める公式 最終更新日 円柱の体積 V は、 円周率× 半径 × 半径 × 高さ 円柱の表面積 S は 2 ×円周率× 半径 × 半径 + 2 ×円周率× 半径 × 高さ このページでは、円柱の表面積について詳しく説明します。 体積の求め方の詳細は 三角柱、四角柱、円柱の体積の求め方 に書いています。立体の体積の求め方 これで,円錐の体積が円柱の体積の 三分の一 になっていることが示されたのですが,以上の議論は,「任意の立体について,基準となる軸に対して軸と垂直な平面による切断面の面積が分かれば,その立体の体積を定積分により求めることができる。 積分を用いた証明 二つ目の説明です。数学2の知識が必要になります。積分を使って V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h を証明します。 底面積の形によらない(円錐でも三角錐でも四角錐でも適用可能)証明方法です。
いろいろな立体の問題
円柱 体積 積分
円柱 体積 積分-面積分と同様に体積分 互いに垂直な場合には、②のh,i,jについて、ヤコビアンは、 (接空間の微小直方体の体積 です) となります。 (1) 直交座標系 原点Oを通り互いに垂直になるように、3本の座標軸、x軸、y軸、z軸をとり、座標をx座標、y座標、z座標の3つの座標の組 で表します。 高校の二つの交差する円柱の領域の体積(重積分) https//youtube/1Hpf_z_XLEc 有名問題!二つの交差する円柱の領域の体積! を高校数学求める動画です
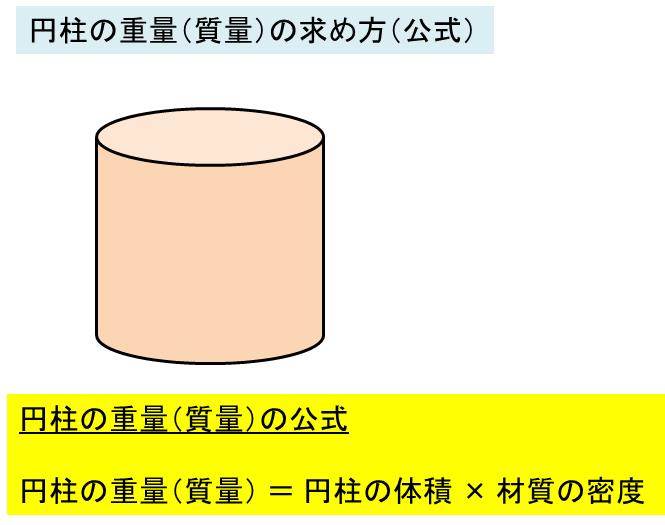



丸棒の重量 円柱の体積と重量の求め方 鉄の場合
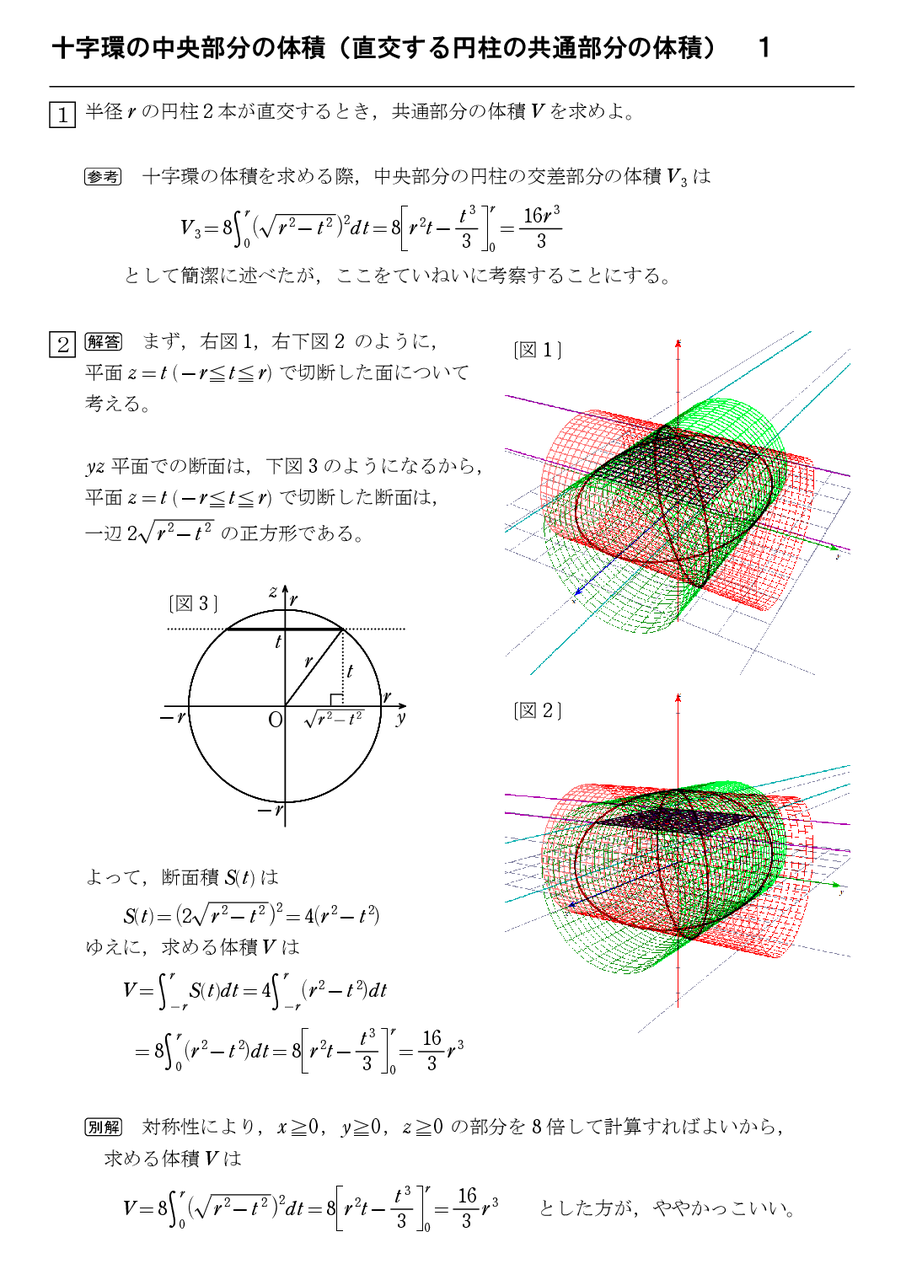
x軸を中心とする半径1の円柱,y軸を中心とする半径1の円柱,z軸を中心とする半径1の円柱の共通部分の体積を求めよ。 (式で表現すると x 2 y 2 ≦1,y 2 z 2 ≦1,z 2 x 2 ≦1の共通部分の体積を求めよ) こうなるとどの軸で切っても同じなのでとりあえずx軸で切断します。 答え 対称性よりx≧0の部分だけ計算して2倍すればよい。 x=tで切ったときの断面は次の通り断面積を積分すると、体積が求めることができるから、求める体積を Vとおくと、この断面積を積分すると、体積が求められるので、 10 ムービー 13 円盤をz軸の周りに回転する。 ムービー 14 断面を積分する。 ・・・(答) 求める立体は、下のような図形となる。 11 ムービー 15 立体の完成よって円柱座標における微小体積 要素 問題①次に示す直方体の体積を三重積分によって求めてみましょう。 ≫続きを読む dv計算法-答え dv計算法-答え ≫続きを読む dvの計算法-ヤコビアンを使うやり方関連ページ 微小面積要素の計算 ある座標系を他の座標系へ変換するときに関数
次元極座標 変数 から への変換 ! 表面積は半径の二乗に比例し,体積は半径の三乗に比例することは感覚的に明らかです。 よって,公式を覚えていなくても S = A r 2 , V = B r 3 S=Ar^2,\V=Br^3 S = A r 2 , V = B r 3 ということが分かります。体積における置換積分を理解していれば次の問題は難しくありません. 例題3 立体A,B,Cをそれぞれ半径の1の直円柱とする.A,B,Cのどの2つの中心軸も直交するとき, 3つの円柱の共通部分の体積を求めよ. すなわち,x軸,y軸,z軸が中心軸である底面の半径1の円柱の共通部分を求めようと
円柱の体積=底面の面積×高さ より, 体積は,4π×2=8π(cm3)となります。 このように,回転体の体積を求めることは中学1年で学習しますが,上の方法とまったくちがう求め方があ ります。その方法を紹介しましょう。 下の図3のように,平面図形をつり下げたとき,その平面図形が水平になっ従って求める体積は底面の半径がa であって高さが2a の円柱の体積 x2 y2, z = に挟まれた部分の体積を求めれば良く、この積分 範囲内では平面が常に 放物面より上にある事に注意すれば V = ZZ x2(y−1 2) 2≤1 4 (y −x2 −y2)dxdy となり、 こで極座標に変換する = Z π 0 Z sinθ 0 ° 不等式で表された立体の体積、直交する円柱の共通部分の体積 スポンサーリンク 高校数学Ⅲ 積分法の応用(面積・体積・長さ) 検索用コード x0,x²y²1,0 z y²\ で表される立体の体積Vを求めよ$ 立体の形状をイメージしようとするのは無理がある



数学 積分を使って面積や体積を計算する方法を分かりやすく解説



写真のような円柱の体積を 微小体積要素 Dv Rdrd8dzを積分して求めたい Yahoo 知恵袋
重量計算の際の体積を求めたかったため ご意見・ご感想 中空円の面積の求め方はS=π÷4((外円の直径×外円の直径)(内円の直径×内円の直径))だと思うのですが、中空円柱では÷4が無いのはなぜでしょうか? keisanより 円の直径 = 2 * 円の半径 より、累次積分 累次積分(続) 累次積分(例と練習) は 次元円柱座標での体積要素である。 問題 以下の各 重積分を求めよ。 答 !• 積分:円柱座標の微小体積要素とデカルト座標の微小体積要素 • 変数ρ、zは距離(長さ)の次元を持つが、変数φの単位はradianである。 ( ) ( ),,,, xyz dV d d dz dxdydz d d dz d d dz z ρρ ρ ρρ ρ φ φφ φ ∂ = →= = ∂ 701-13 701-14 円柱座標(7) 計量テンソル: metric tensor 直交基底:規格化しない



円柱の斜め切断
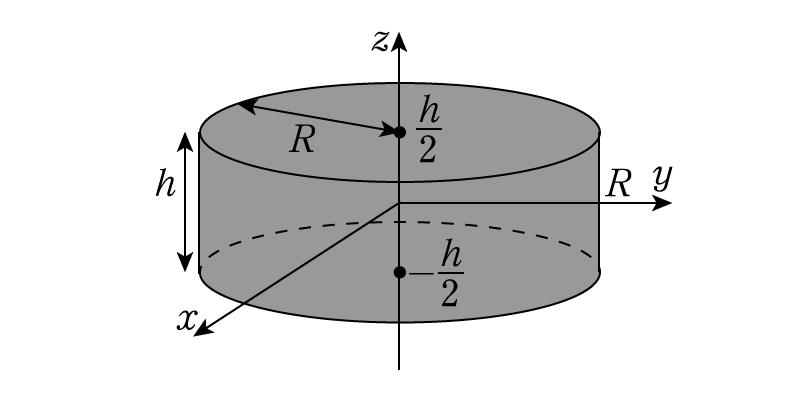



剛体の慣性モーメントの計算 物理の学校
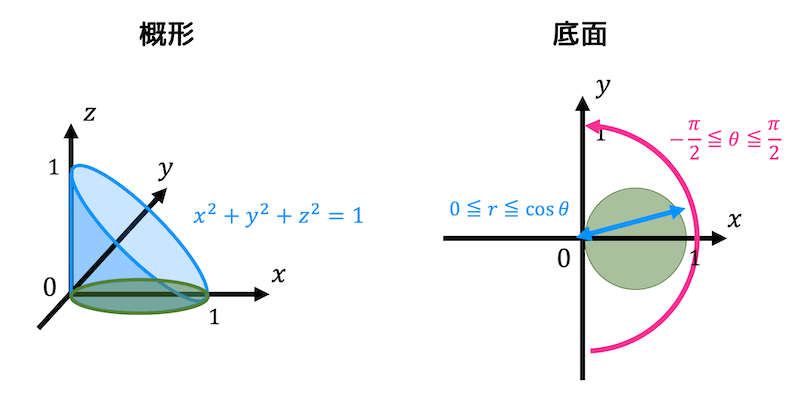
体積の導出 円柱の体積 \( V \) は\V = 2 \iint_D \sqrt{1 x^2 y^2} \\D = \{ (x,y) \mid x^2 y^2 \leqq x \} \で求めることができる。 積分範囲を変換するため、極座標変換\x = r \cos \theta , \ \ \ y = r \sin \theta \\ \left( r \geqq 0, \ \ \pi \leqq \theta \leqq \pi \right) \を行う。円柱の体積 通常、この問題は、高校2年で学習する「数学II」の微分積分の格好の応用問題として、 教室で取り上げられることも多いことだろう。 (解) S=2πr 2 +2πrh より、 2πrh=-2πr 2 +S なので、 y=2V とおくと、 y=r(-2πr 2 +S)=-2πr 3 +Sr となる。 よって、確かに、 y = ±√R2 − x2 ⋅⋅ ⋅(2) y = ± R 2 − x 2 ⋅ ⋅ ⋅ ( 2) とすると あるx x の値に対してy y の値が2つ出てきます 。 これでは積分が実行できないので、記号だけ使います。 y = √R2 − x2 ⋅⋅ ⋅(3) y = R 2 − x 2 ⋅ ⋅ ⋅ ( 3) そうすると関数として扱うことができるので積分が実行できます。 求める面積は図のように上半分の面積を求めて2倍すれば良い ことになり




定積分の応用
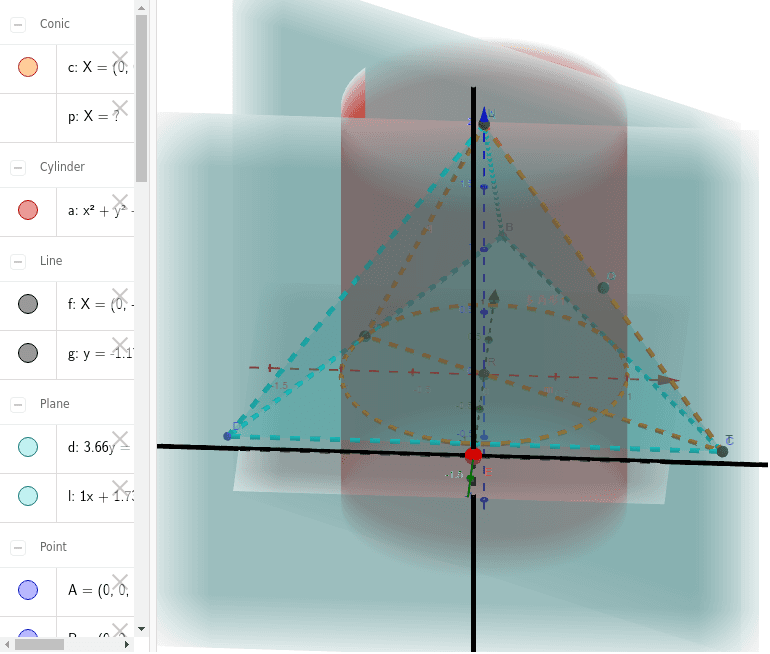



円柱の外の四面体の体積 Geogebra
体積3 17年12月15日 19年2月8日 次もよくある問題で、柱体の共通部分の体積を求める問題です。 まずは円柱と円柱から。 より基本的な問題は数学Ⅱの体積の方にあります。 1. B (東北大) 空間において,半径が1で 軸を中心軸として原点から両側に無限と表すことが出来た。3 次元でも同じ様に空間を分割することによって積分を定 義するので、同様のことができる。 例131 球x 2 y z2 • a2 と円柱(x ¡ a 2)2 y2 • (a 2)2 の共通部分D の体積 を求めよ。 解 求める体積は対称性からD\fy ‚ 0;第1節 体積における置換積分を身につけよう(その1) ここでは,積分を用いていろいろな体積を求めます. A,Bをそれぞれ半径の1の直円柱とする.A,Bの中心軸が直交するとき, 2つの円柱の共通部分の体積を求めよ. この問題は,2つの円柱の中心軸をそれぞれx軸,y軸とし,z軸に垂直な平面z



積分の問題です 半径rの直円柱がある この円柱を 底面の直径abを通り Yahoo 知恵袋




丸棒の重量 円柱の体積と重量の求め方 鉄の場合
<円柱貫通体について> 積分を応用して円柱貫通体の体積Vを求める。 2本の円柱が交わった部分の立体の体積を求める有名な問題でが、高校生3年生時に説明を聞くまでは、立体 の形がイメージできなかったのではないでしょうか?つまり、立体の存在自体に詐欺があります。以下に4つによって、 空間における領域 が 空間の領域 " にうつるとき、 が成り立つ。ここで、 は 次元極座標での体積要素である。 問題 以�円柱の体積 円柱の体積の公式より, V = π r 2 h = π × 1 2 × 1 = π 円錐の体積の公式を用いた場合 円錐の体積の公式より, V = 1 3 π r 2 h = 1 3 π × 1 2 × 1 = π 3 定積分の公式を用いた場合 定積分の基本式より, ∫ a b f (x) d x = F (x) a b = F (b) − F (a) ( F (x) は f (x




体積 11 円錐と円柱の共通部分 怜悧玲瓏 高校数学を天空から俯瞰する
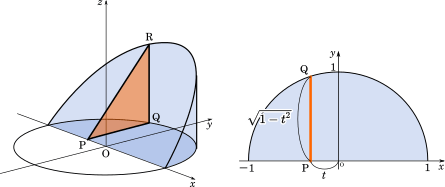



数 積分 円柱を斜めに切った立体の体積を求める Mm参考書
円柱の斜め切断を行い,その体積と断面の描く曲線と側面積とが,三角関数で面白く表現できるということをまとめたつもりである。 2 西元先生の対称性のある関数の定積分とは 西元先生の研究によると,「すべての実数αにおいて, である。」ことが 円柱座標系で積分する方法 円柱座標系の体積要素 円柱座標系での体積要素は \ dV = r dr d\theta dz \ です。 円柱の体積を求めてみると まず手始めに半径\(R\)、高さ\(h\)の円柱の体積の計算を円柱座標でしてみます。 円柱と球面の囲まれる部分の体積曲面積を求める問題で 数学 曲面積 数学 4 2重積分を利用して体積を求めよ。 数学 5 球と円柱の共通部分の体積 数学 6 e^(x^2)の積分に関して 数学 7 重積分がわからない、、 数学 8 積分で1/x^2 はどうなるのでしょうか? 数学 9 ∬1/√(x^2y^2)dxdy




体積の求め方 回転体ではない立体を積分で 数学の偏差値を上げて合格を目指す



Http Www Din Or Jp Saigou Math Sagi24 Pdf
5(8)(立体の体積4) 次の各曲面で囲まれた立体の体積を求めよ. (1)球面x 2y z2 = a (a > 0)で囲まれた円柱面x2 y2 = axの内部D. (2)放物面x 2y = z と柱面x y2 = 2z で囲まれた部分E. (3)曲面z 2= 4ax (a > 0)と柱面x y2 = axで囲まれた部分F.例 364(円柱の体積) 底面の半径 ,高さ の円柱の体積は である. これを多重積分で求める. (その 1) 円柱の底面が 平面にあるとし, とおく.円柱の上面は平面 である. 円柱の体積は と求まる. ただし, とする. (その 2) 円柱の領域はの公式で求めることができる. この公式は,円柱の体積の公式 V = πr2h V = π r 2 h に 1 3 1 3 をかけたものと考えることができるが,なぜ円柱の体積に 1 3 1 3 をかけることにより円錐の体積が得られるのかを, 定積分法 と 区分求積法 を用いて説明する.




高校数学 非回転体の体積 円柱の切断 受験の月




球体の体積 積分で求める方法 うちーノート
Viviani曲線 球と円柱の共通部分の体積 慶応大91年の問との相違点は球のふくらみ部分(上図の赤い部分)が付け加わったことです。 このことで計算は格段に難度を増しています。元のものが直接には分からなくても,その微分が分かれば,積分 に てできる立体の体積を とし,右図の水色で示した長方形を直径のまわりに回転してできる円柱の体積 を とするとき, を求めてください.(すなわち,平面を回転させたときの円柱の体積よりもどれだけ増えるか) 解説これを、 k=-1~1で積分して体積が得られる。 すなわち、 2 3つの円柱の場合 円柱の中心軸を x、y、z とし、原点で直交しているものとする。このときでき上がる物体
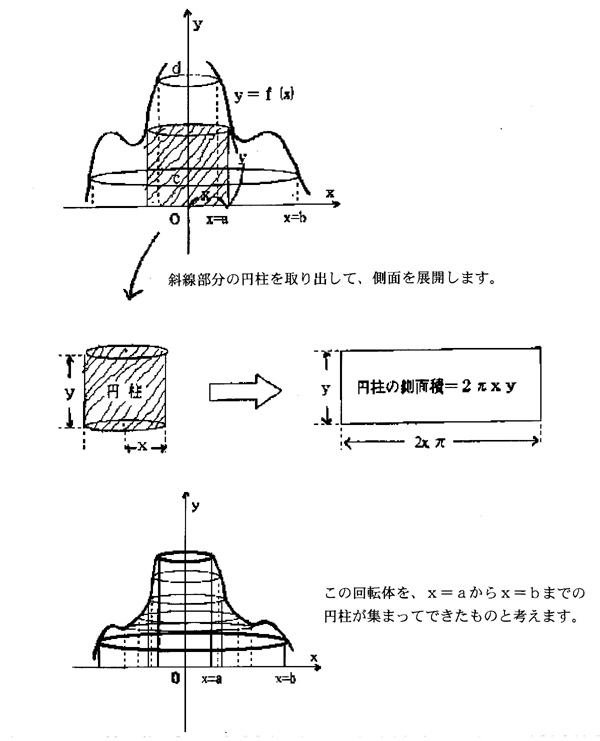



高校数学 バームクーヘン積分




角錐や円錐が 角柱や円柱の体積の3分の1であることを積分 極限抜きで証明してみる
数学検定1級はこれだけで合格できる。 top > 数検1級の重積分 > 重積分3の解説(球と円柱の共通部分の体積)Z ‚ 0g の部分の体積の三角錐体の体積=四角柱×1/3 ではだめ? s:どうして1/2ではないの? t:積分の法則を使うと、 2 (1/2x 2 )'=x 2 dx=1/3x 3 (1/3x 3 )'=x 2 となるから。 s:難しすぎて、意味がわからない。 t:うーん。では究極の万能公式を出そう! 6、シンプソンの



1




円錐と円柱の重なり部分の体積を求める問題です Okwave
これを積分で積み上げていきましょう。$t$ は$1$ から $1$ まで変化していくので、求める体積の式はこうなります。 $\displaystyle\int_{1}^{1} \frac{1}{2}(1t^2)\enspace dt$ 今回の立体は左右対称の形をしています。そこで、積分区間を半分にして、その結果を2倍しても同じことになり問 3 58 (体積の計算) 2 つの円柱 の共通部分 の体積 を求めよ. 次 312 曲面積 上 3 多重積分 前 310 3 次元極座標への置換積分 (円柱の体積)=(底面の円の面積)×(高さ)=πr 2 ×h= πr 2 h 円柱の体積を求めるには、与えられた半径や高さをこの公式に代入すればよいのです。上の基本問題をこの公式を使って求める (1) r=5、h=10 だから、V=π ×5 2 ×10=250π cm 3



いろいろな立体の問題
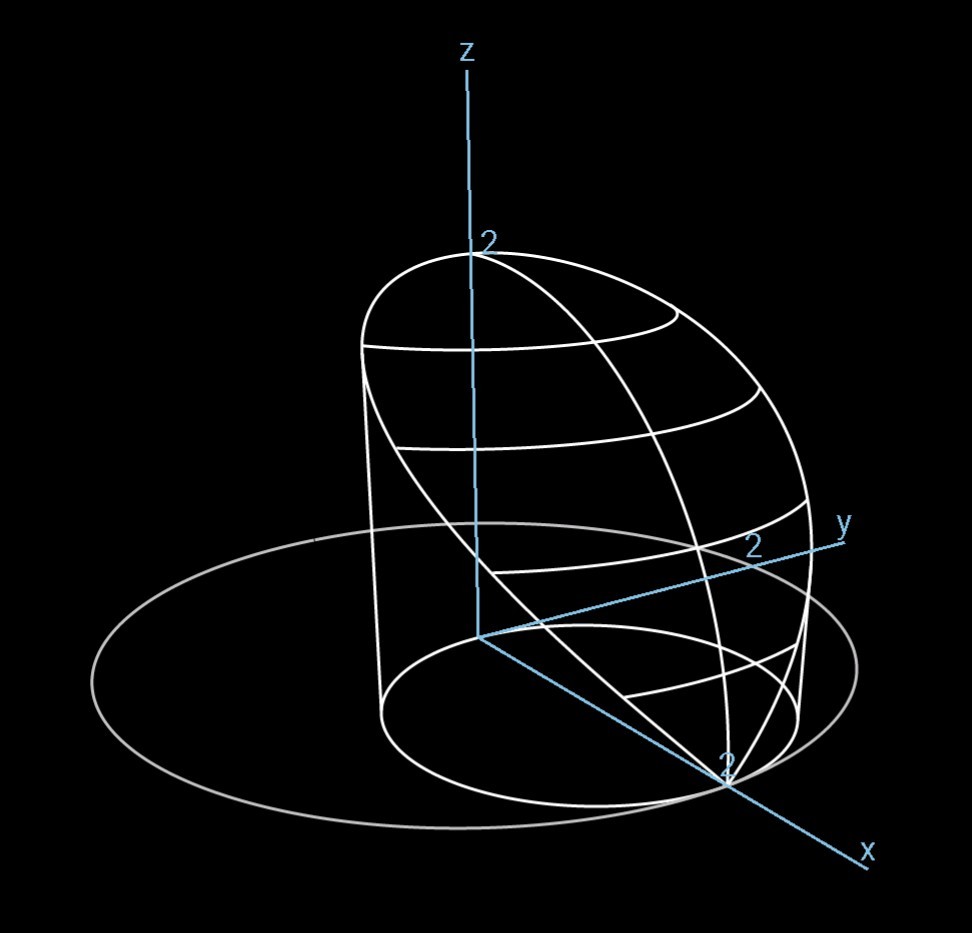



2 半球と円柱の交わりの体積を で求める 齊藤数学教室 算数オリンピックから大学数学入門
この立体は,直線 に沿ってできていますので, となります。 したがって,円柱の体積は,定面積×高さ ですから,微小区間の体積 dV は,1 第1章 基礎事項 11 微分積分 偏微分 変数x, y, z の関数f = f(x,y,z)について ∂f ∂x) yz = lim ∆x→0 f(x∆x,y,z)−f(x,y,z) ∆x (11) をf のxによる1階の偏微分という y, z による偏微分についても同様に 定義する ここで, 左辺の()につけた添え字yz は偏微分を行うさいにy, z を一定とみなすことを意味する多くの場合,計算は2段階に分けて行われる(逐次積分) ˇˇ D f(x,y)dxdy = ˇ b a ˇ φ2(x) φ1(x) f(x,y)dy dx (323) ここでy = φ(x)は積分領域D の境界を表す曲線である.同じ式は次のようにも書か れる ˇˇ D dxdyf(x,y)= ˇ b a dx ˇ φ 2(x) φ1(x) dyf(x,y) (324) 例:原点を中心とする半径aの球の体積. 積分




大学数学 重積分




球の表面積と体積の公式 数学fun
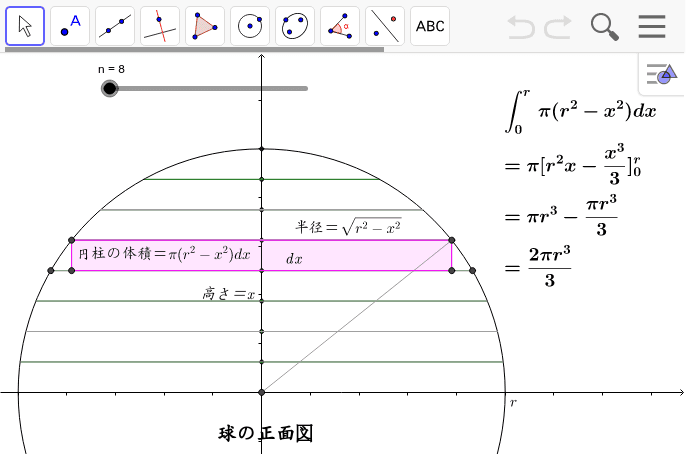
Diva = 3x2 6zであるから, Vは円柱の内部とするとガウスの定 理より ∫∫ S andS= ∫∫∫ V divadxdydz = ∫∫∫ V (3x2 6z)dxdydz 円柱座標 x= rcos ;y= rsin ;z= z (0 ≦ r≦ 1;0 ≦ ≦ 2ˇ) で変数変換すれば ∫∫∫ V (3x2 6z)dxdydz= ∫ 1 0 ∫ 2ˇ 0 ∫ 1 0 3(rcos )2 6zrdrd dz = 15 4 ˇ 考え方 円の上半分のみを考える. x 軸中心に回転させると球ができる 回転する前と後の関係を図式化した. 回転した後の部分を円柱と捉えると,体積は以下のように表される. V1 = y2π × x この厚さが微小な円柱を積み重ねれば球ができる. ・厚さをより微小に x → dx ・積み重ねる= 積分 する



体積積分 交差立体 京極一樹の数学塾
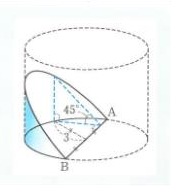



数学を極める 1 積分 数 を極める 体積編 予備校なら武田塾 河内松原校
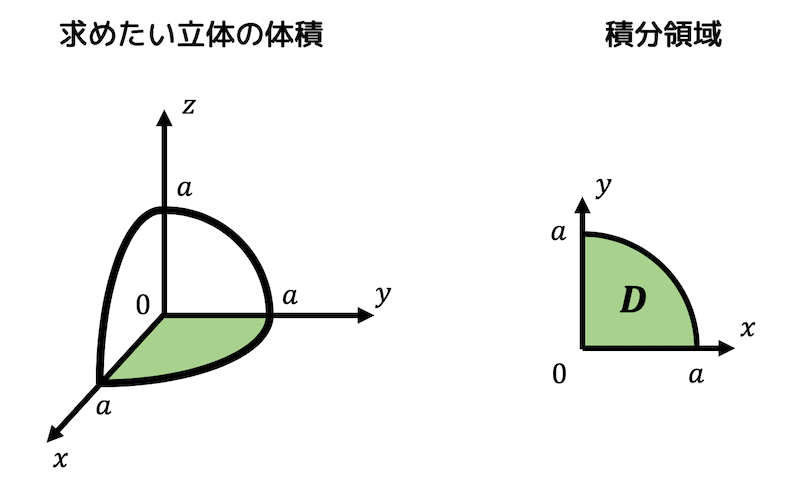



うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾



数学 積分を使って面積や体積を計算する方法を分かりやすく解説



いろいろな立体の問題




円柱の表面積と体積を求める公式 具体例で学ぶ数学



体積積分例題 Of 京極一樹の数学塾




ねこ騙し数学
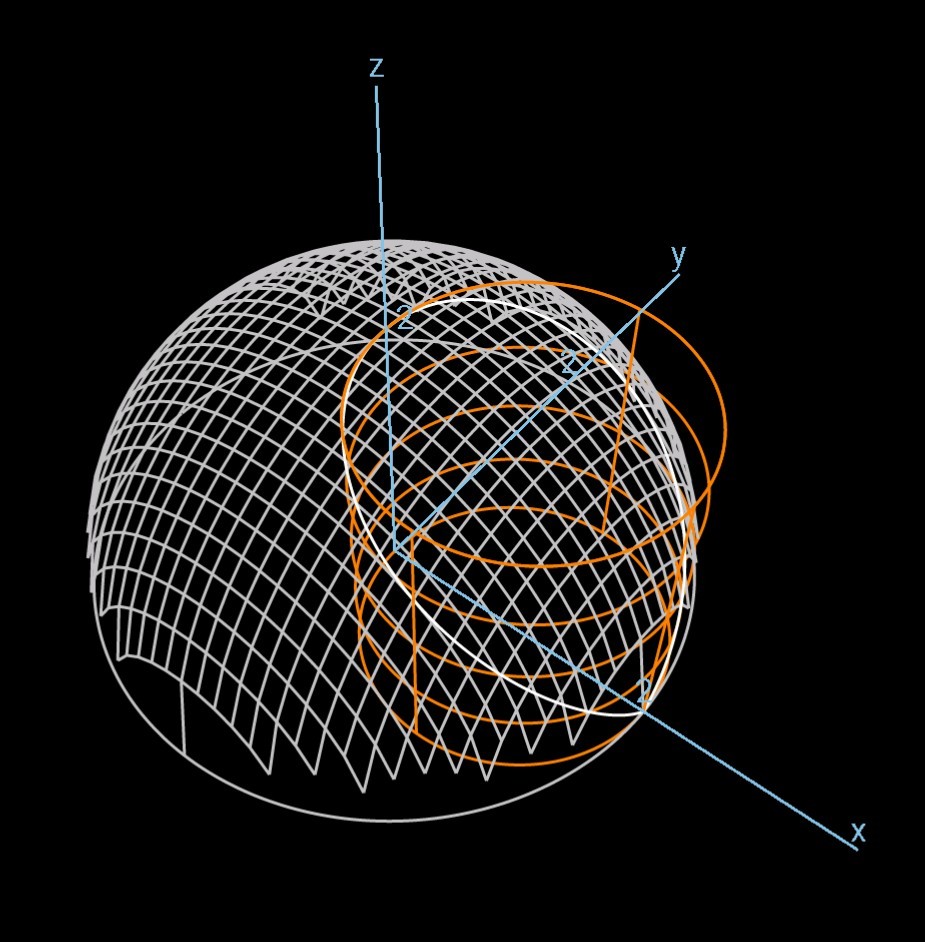



2 半球と円柱の交わりの体積を で求める 齊藤数学教室 算数オリンピックから大学数学入門



しょうちゃん 公式ブログ 算数の問題を解いてみる その45 円すい 体積 積分 丸暗記 Powered By Line




高校数学 円筒分割積分 バウムクーヘン分割積分 V 2p Xf X Dx 受験の月
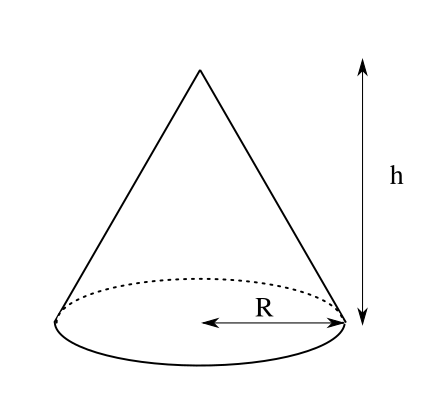



円錐の体積を円柱座標系で真面目に計算してみた ゴルディアスの涙目




この中で2重積分でできるものをやってもらえませんか この中で2重積 数学 教えて Goo




バウムクーヘン積分 おいしい数学




数 積分 円柱を斜めに切った立体の体積 2 四角形の積分を用いる 底面が楕円 Mm参考書



体積積分 Of 京極一樹の数学塾会員頁




うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾
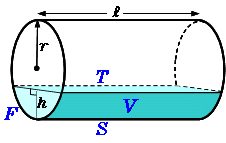



一部が欠けた直円柱の体積 高精度計算サイト



円柱の体積
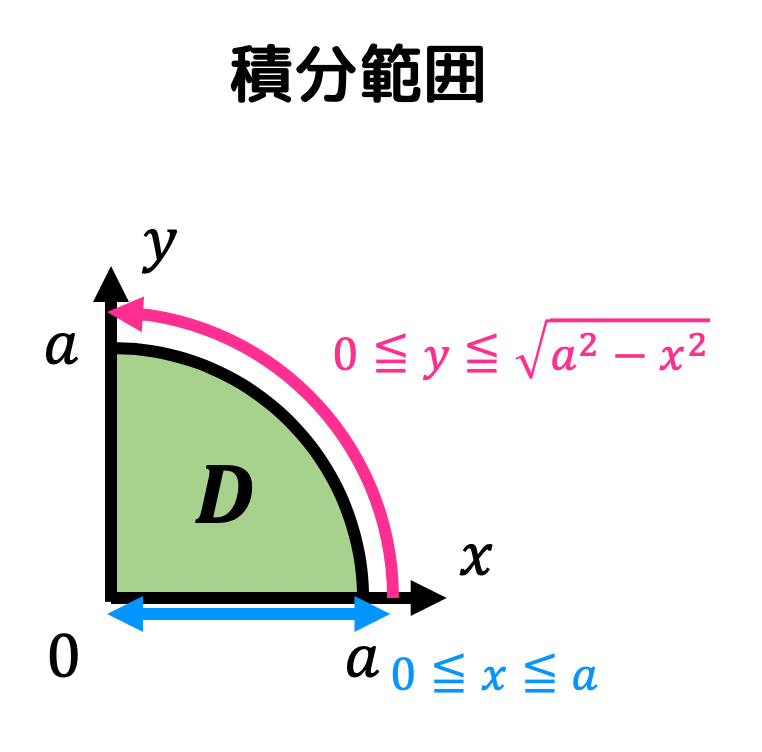



うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾




角錐や円錐が 角柱や円柱の体積の3分の1であることを積分 極限抜きで証明してみる




重積分5 三つの交差する円柱の領域の体積 数学 微分積分学 Mathematics Youtube




高校積分で 三つの交差する円柱の領域の体積を求めます 数学 微分積分 Youtube



3 13 体積の計算



Http Www Shimanet Ed Jp Minami Link Homepage Naga005 Grapes 001 Enchuu2ko Pdf




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




非回転体 交差する円柱の共通部分 Steinmetz Solid 理系のための備忘録
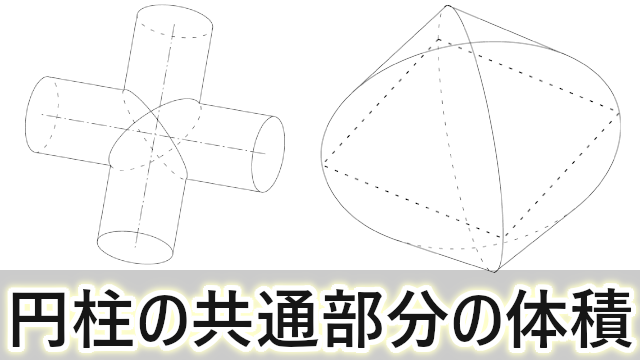



円柱の共通部分の体積 非回転体の体積 大学入試数学の考え方と解法



3 13 体積の計算



数 積分の問題です 底面の半径がaで高さもaである直円柱がある こ Yahoo 知恵袋



不可思議な立体



1




定積分の応用



いろいろな立体の問題
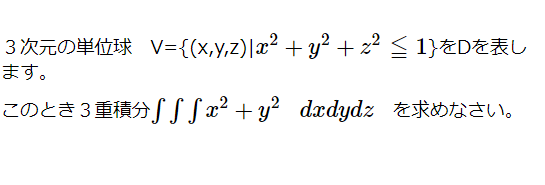



重積分3の解説 球と円柱の共通部分の体積 数学検定1級はこれだけで合格できる



立体の体積計算 積分 高校 理数系無料オンライン学習 Kori
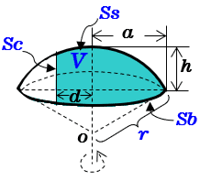



一部が欠けた弓形の回転体の体積 高精度計算サイト




体積 10 球と円柱の共通部分 怜悧玲瓏 高校数学を天空から俯瞰する




Hashtag 積分 Auf Twitter



切頭円柱の体積を定積分で求める定番の問題ですが 画像右のように8で断面積を表し Yahoo 知恵袋



円錐の体積を円柱座標系で真面目に計算してみた ゴルディアスの涙目




ねこ騙し数学




電気磁気工学を学ぶ 円錐の体積 積分



3 13 体積の計算



いろいろな立体の問題



体積積分 交差立体 京極一樹の数学塾




書記が数学やるだけ 29 体積をいろんな積分で解く 鈴華書記 Note



いろいろな立体の問題




青チャート数3積分問題です Clear
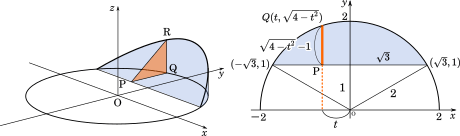



数 積分 円柱を斜めに切った立体の体積を求める Mm参考書
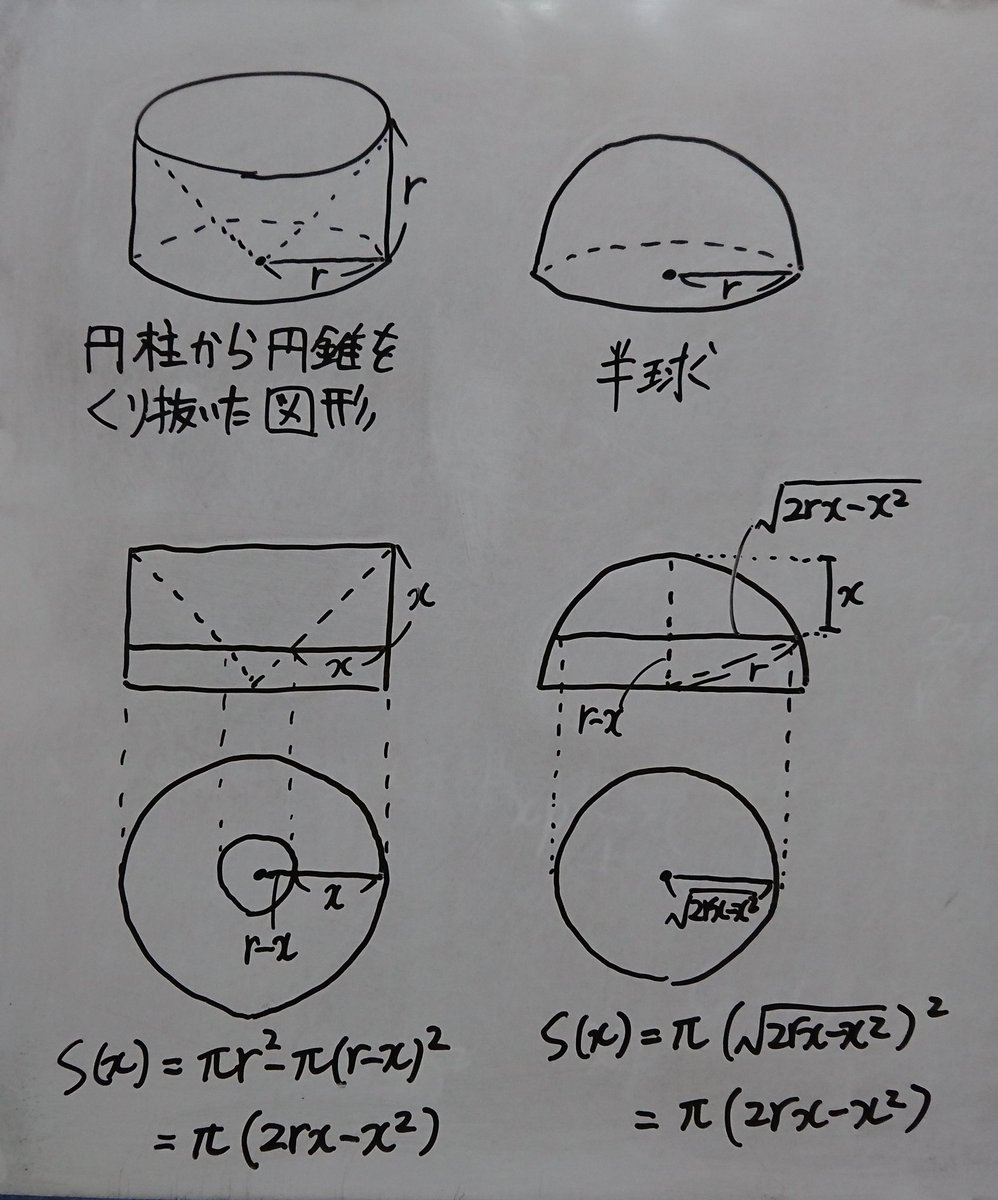



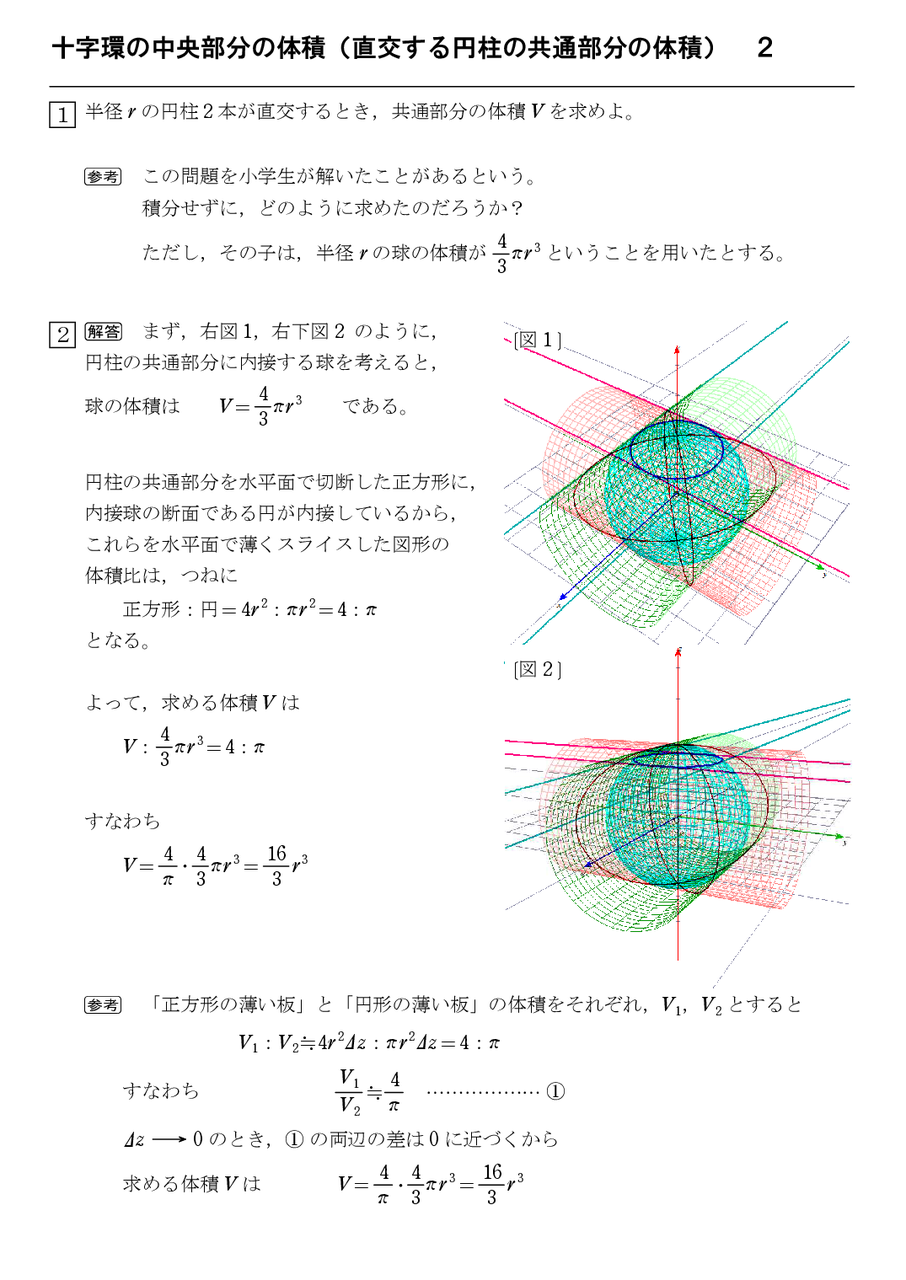
バラノラ Di Twitter 積分を使わずに球の体積 円柱から円錐をくりぬいた図形と半球の各高さにおける断面積が等しいことから球の体積が4 3pr 3だとえいる でも円錐の体積が円柱の体積の1 3と等しいことは仮定しちゃってるから微妙かも
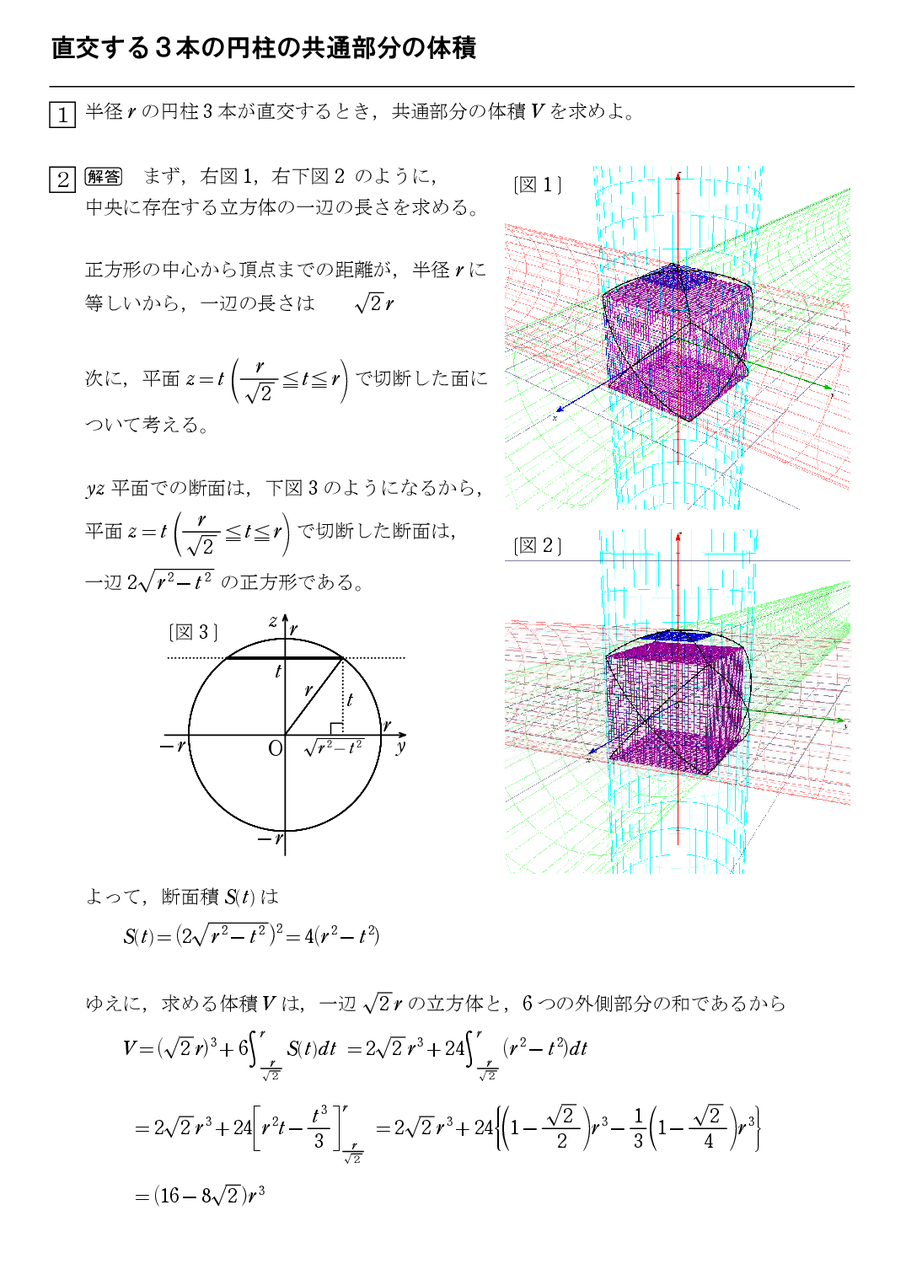



直交する3本の円柱の共通部分の体積 怜悧玲瓏 高校数学を天空から俯瞰する



円柱とは 体積 表面積の公式や求め方 単位あり計算問題 受験辞典



Http Www Shimanet Ed Jp Minami Link Homepage Naga005 Grapes 001 Viviani All Volume005 Pdf



積分計算による体積の求め方 断面積の積分や回転体の体積 受験辞典



体積積分 交差立体 京極一樹の数学塾




円柱の表面積と体積を求める公式 具体例で学ぶ数学




円すいのときの体積の求め方の公式と 球の体積の求め方の公式を教えてください Clear




大学数学 25 立体の体積



1



十字環の中央部分の体積 直交する円柱の共通部分の体積 1 怜悧玲瓏 高校数学を天空から俯瞰する




X軸についての回転体の体積の求め方とコツを分かりやすく解説
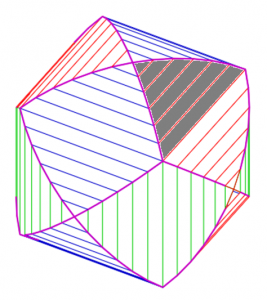



非回転体 交差する円柱の共通部分 Steinmetz Solid 理系のための備忘録



うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾




高校数学 平面図形の回転体の体積 受験の月




円柱座標系でのbの積分区間が2枚目のようになるのがわかりません 教えてください Clear




三重積分の計算ー円柱座標 極座標のヤコビアンと変数変換



十字環の中央部分の体積 直交する円柱の共通部分の体積 2 怜悧玲瓏 高校数学を天空から俯瞰する




3つの直交する円柱の共通部分の体積 数学の偏差値を上げて合格を目指す



球の体積の積分 Geogebra



2重積分の問題です Xy平面上の円x Y A を底面 Yahoo 知恵袋




3次元空間の直交座標 円柱座標 球座標2 座標変換に関する問題 身勝手な主張



1




数 積分 円柱を斜めに切った立体の体積 2 四角形の積分を用いる 底面が楕円 Mm参考書




重積分4 二つの交差する円柱の領域の体積 数学 微分積分学 Youtube




缶詰 円柱 の中に入れた水をこぼすと てっぃちmarshの数学 Mathematics 教室




積分の区域と奇関数と偶関数 の質問です Clear
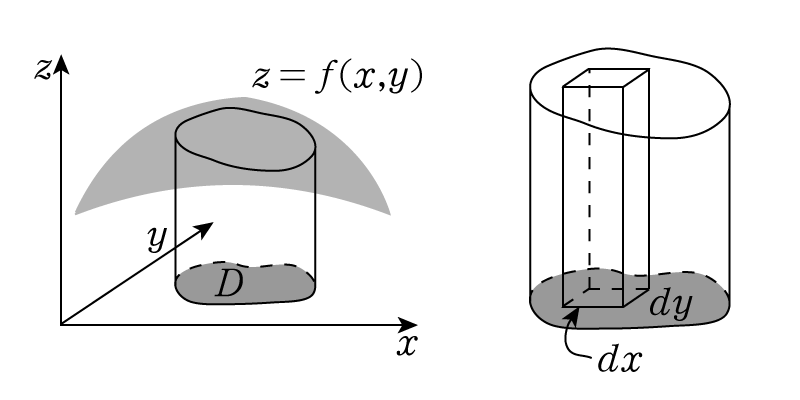



多重積分の極座標変換 物理の学校
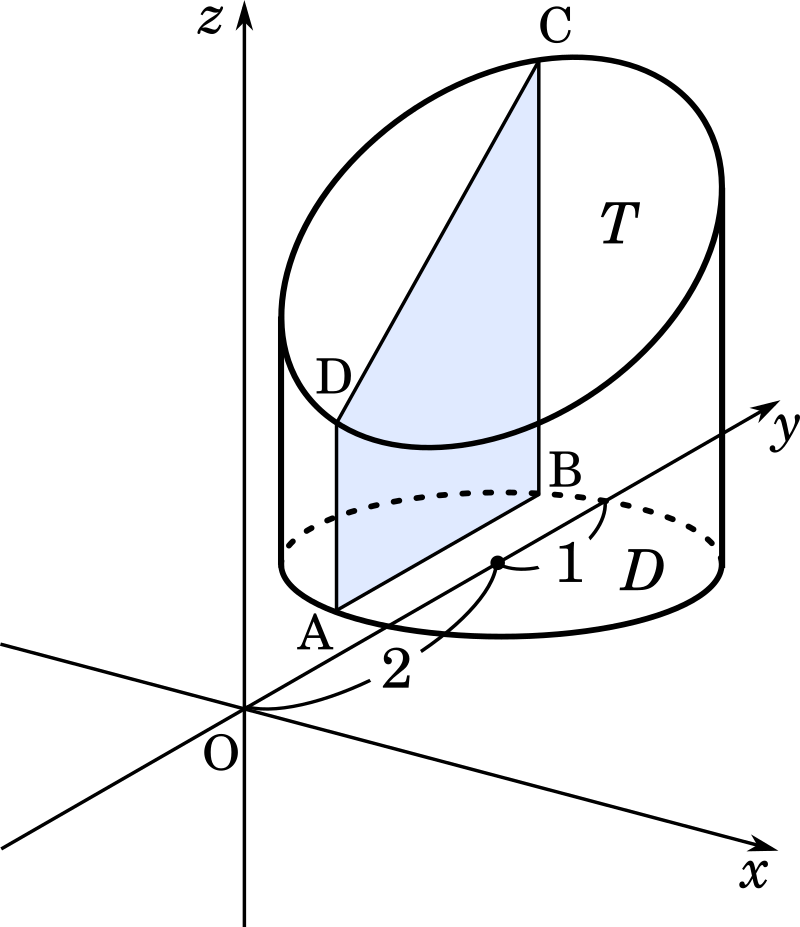



数iii積分 円柱を斜めに切った体積とドーナツ回転体 断面が台形 九州大 Mm参考書



大学入試問題を考える Ssブログ
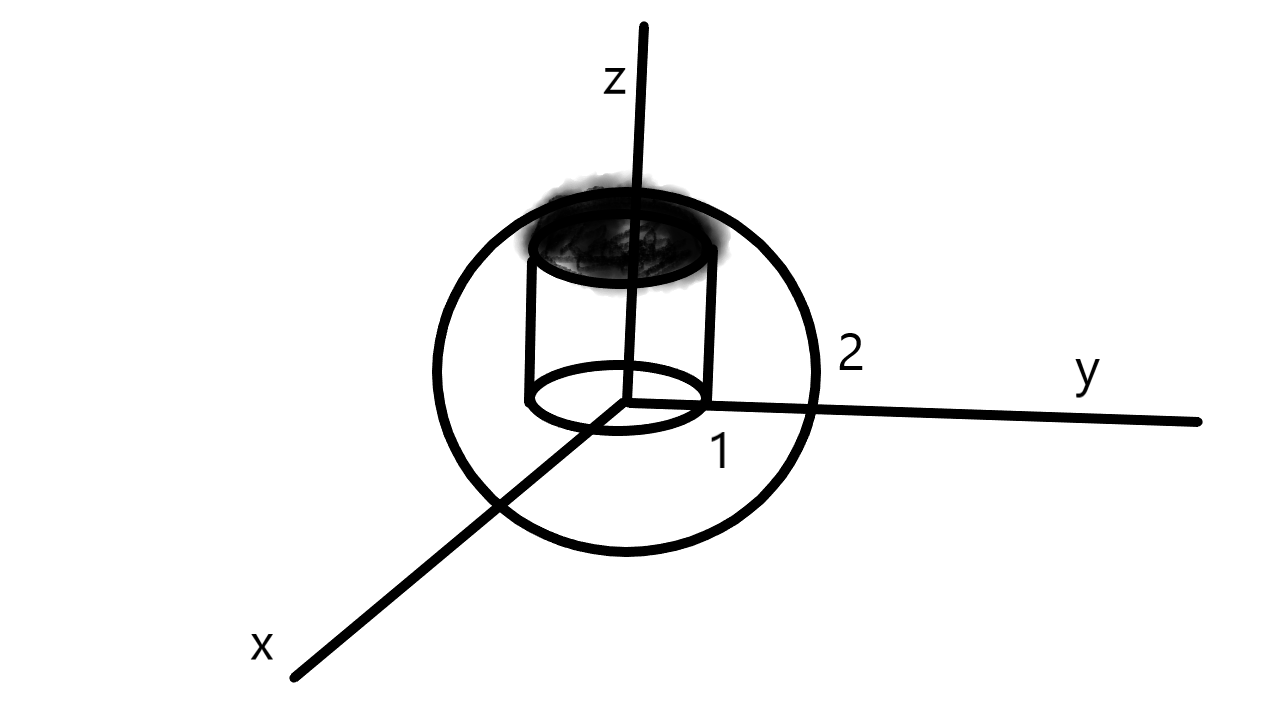



重積分3の解説 球と円柱の共通部分の体積 数学検定1級はこれだけで合格できる




重積分の問題です 円柱面x 2 Y 2 1と平面z Xで囲まれた部分の体積を重 数学 教えて Goo



0 件のコメント:
コメントを投稿