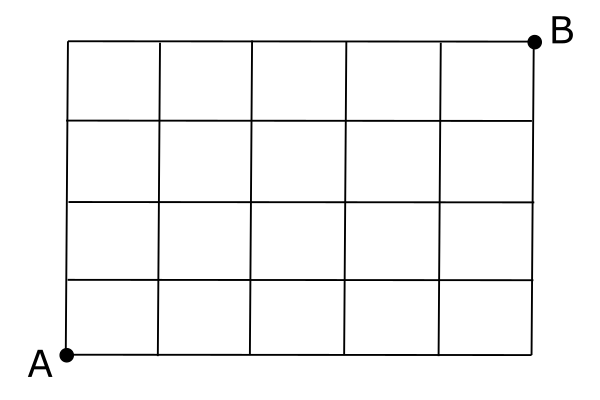
家から学校までの通学路が何通りあるかを求めよう まずは途中に病院があって, 家から病院までの道が 通り, 病院から学校までの道が 通り ある場合, 通学路の総数は 通り このように, つの分岐点を通過するとき, 前後の経路数をかけ算 すればよい 和の法則 次に, 家から学校までの道に病院と薬局がありどちらかの経由でしかいけない場合 家から病院まで 通りの道があるが, そこから学校までは 本
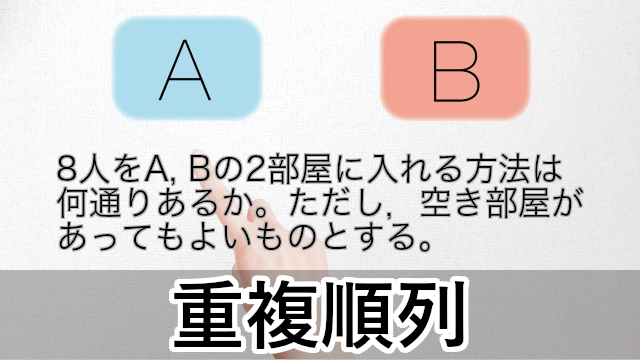
何通りあるか 数学-高校数学Aで学習する場合の数の単元から 「硬貨を使って支払える金額は何通り? 」 について、パターン別に解説していきます。 取り上げる問題はこちら! 問題①(使わない硬貨があってもよい) 500円,100円,10円の3種類の硬貨がたくさんある。 この3種類の硬貨を使って,10円を支払う場合の数を求めよ。 ただし,使わない硬貨があってもよいものと★次の硬貨の一部または全部でちょうど支払うことのできる金額は何通りあるか。 <人(物)を並べる場合の数 例題> ★次のように1列に並べる並べ方は何通りあるか。 <役割を選ぶ場合の数 例題> ★次のように役割を選ぶ方法は何通りあるか。
何通りあるか 数学のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  |  |
 |  |  |
「何通りあるか 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
「何通りあるか 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | 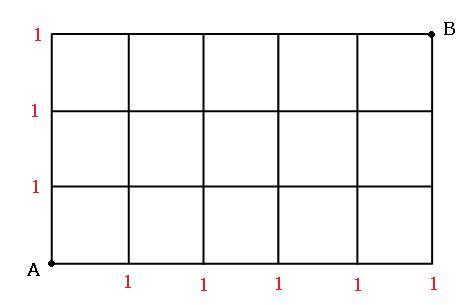 |
 | ||
 | ||
「何通りあるか 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 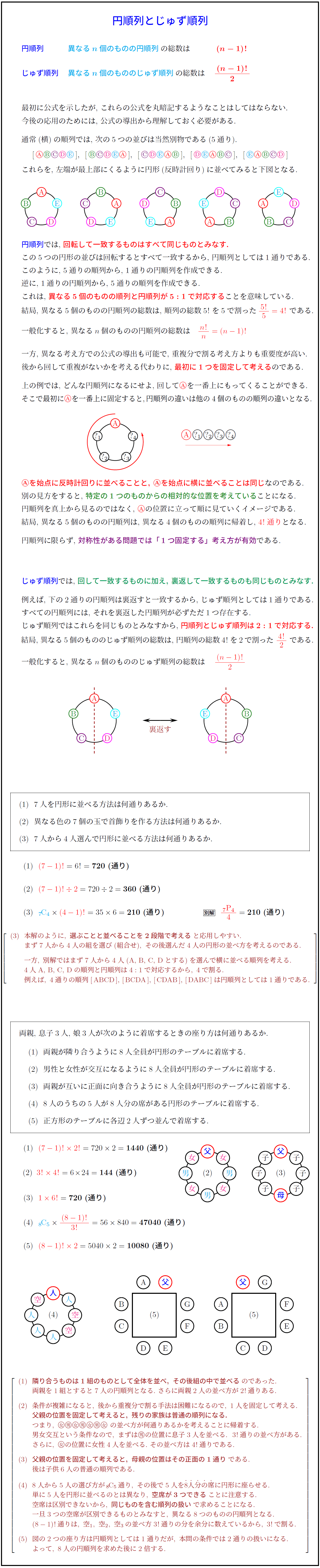 |
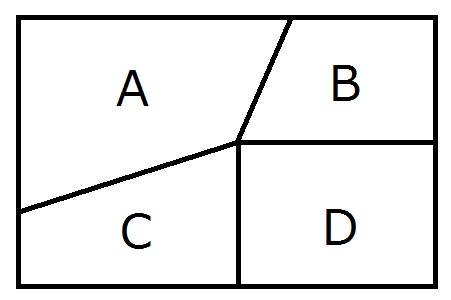 | 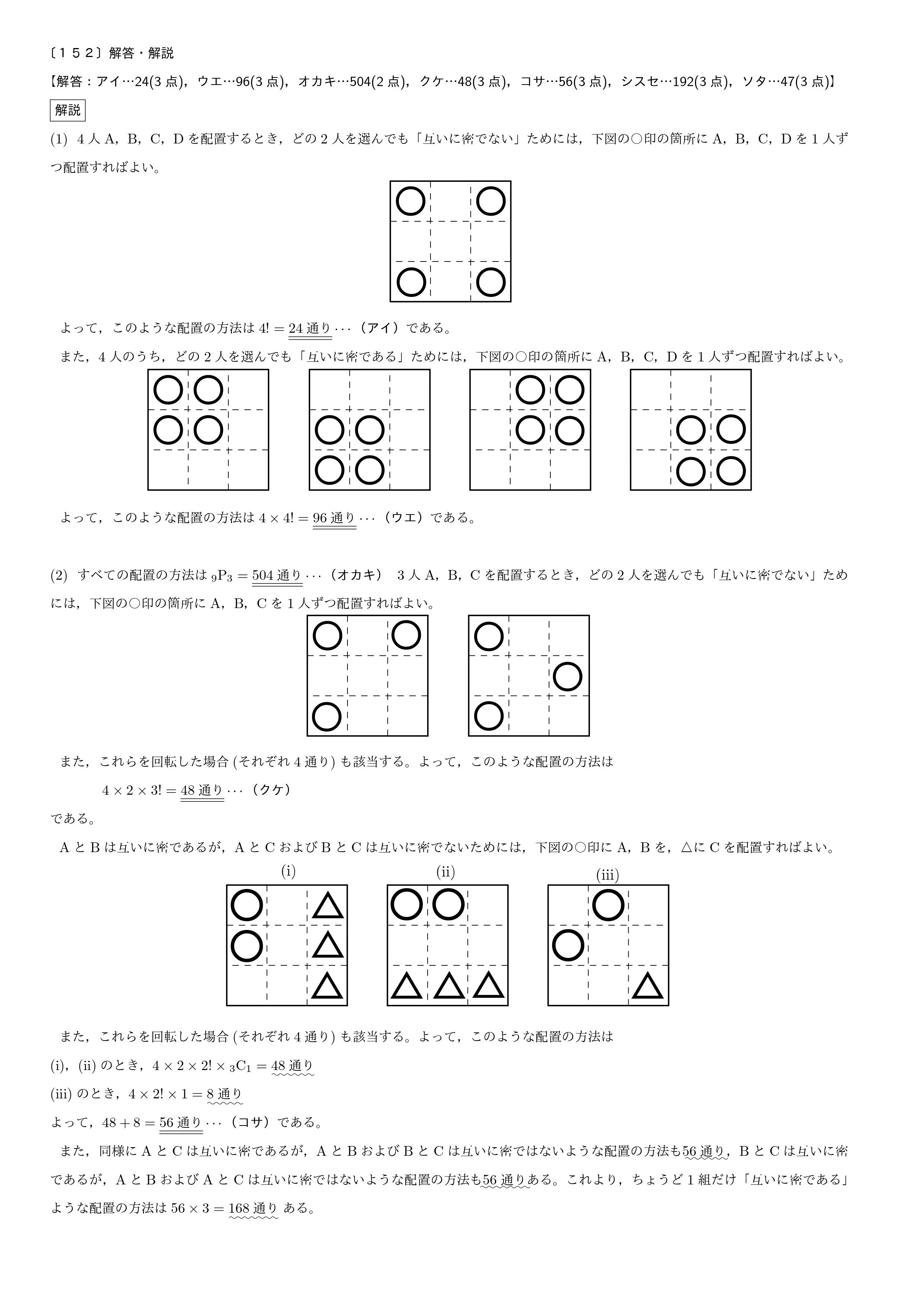 | |
 |  | 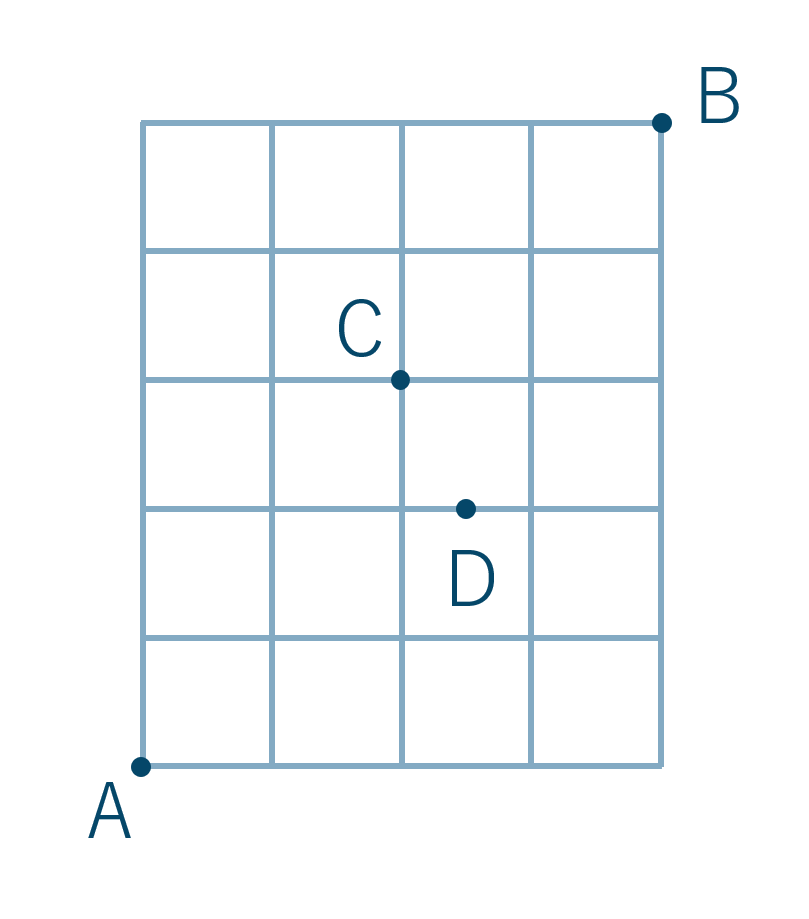 |
 |  | |
「何通りあるか 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | 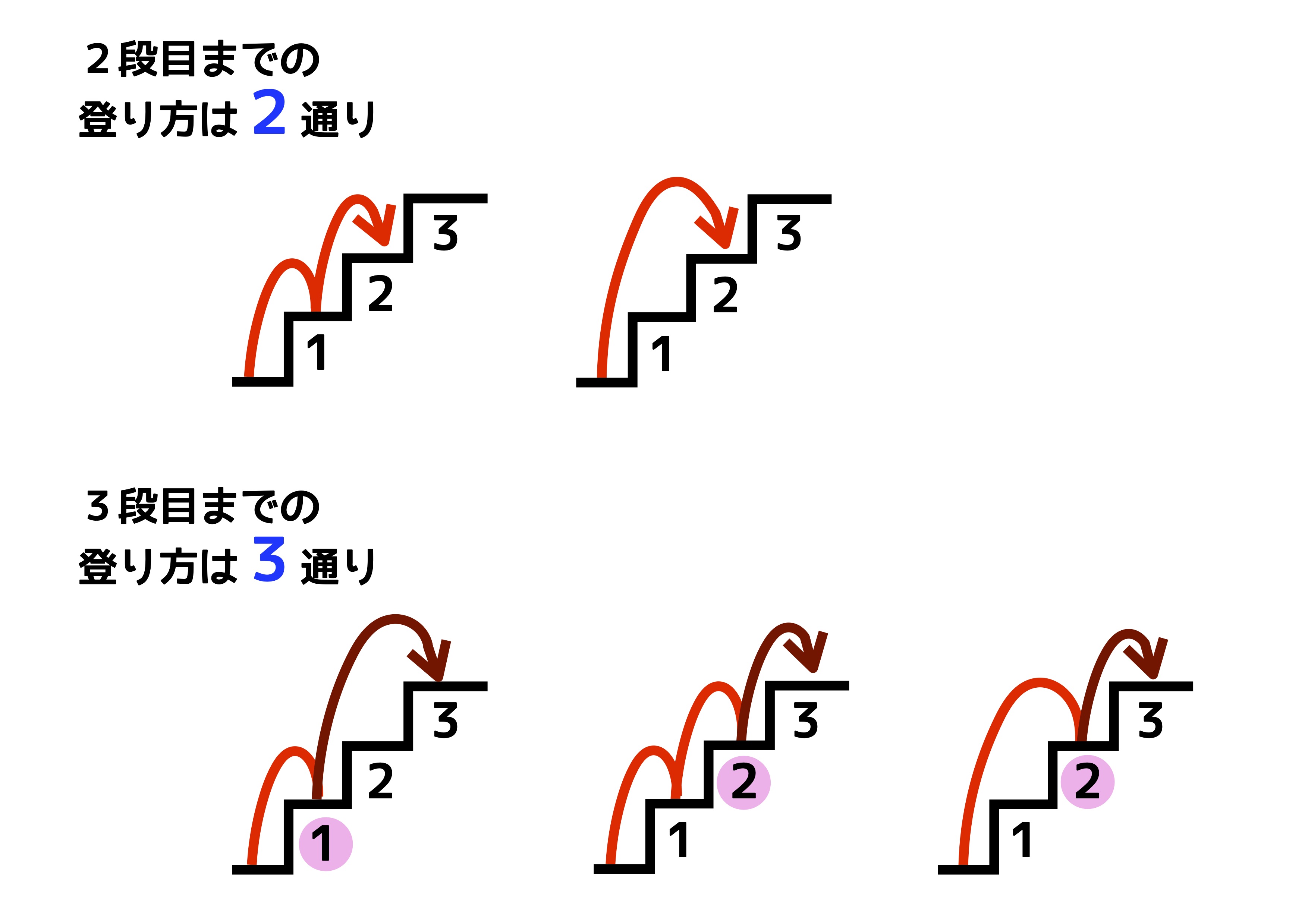 |
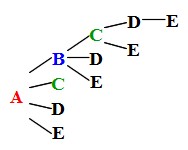 |  | |
 |  |  |
「何通りあるか 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  |  |
「何通りあるか 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「何通りあるか 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「何通りあるか 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |
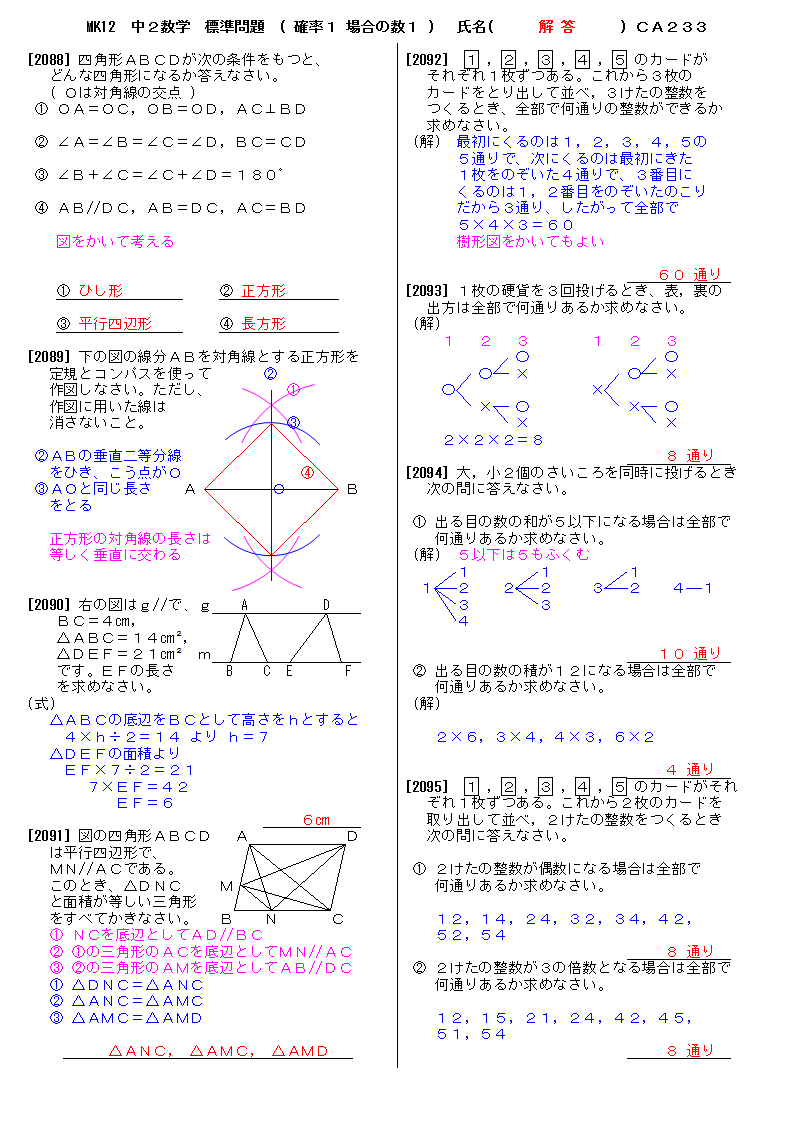
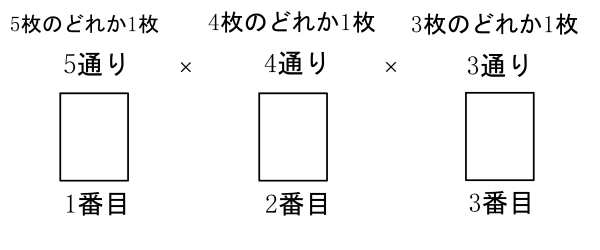
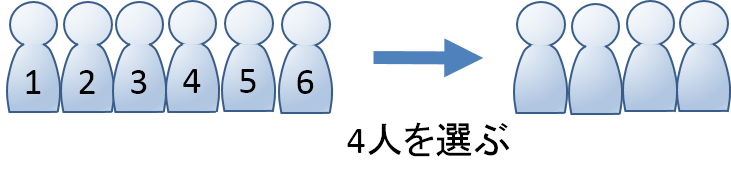
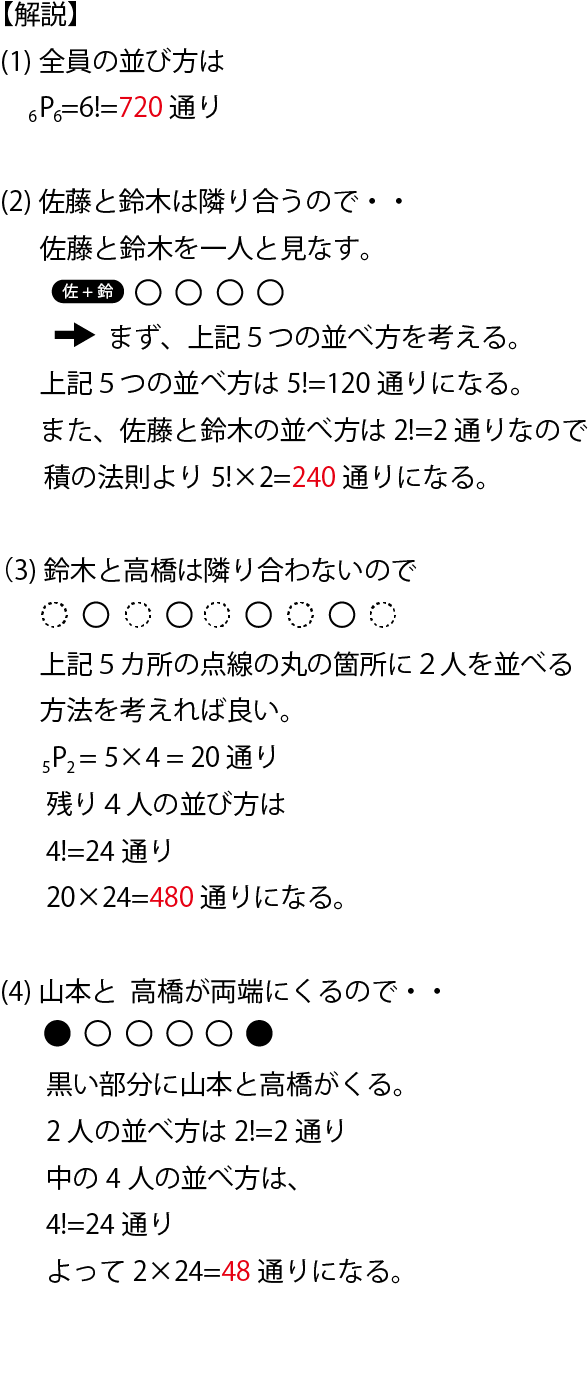
アルファベット A が 個、B が 個あるとき、その並べ方は何通りあるか。 並べるものの種類と個数が決まっており、その中に同じものを含むので「同じものを含む順列」です。 解答 答え: 通り 公式を使って簡単に求められましたね。 論理的に考えれば、 か所から を入れる か所を選ぶことになるので、 と計算できます。 これを展開すると、 となります。 同じもの 種類を含む順列は、組3(2)100円以下になる組み合わせは何通りあるか求めなさい。 3(1)と同じように数えますが、100円と500円までかぞえると100円以上になってしまいますので、100円と500円を除いた4枚の組合せをかぞえる‥ということになります。 1円を基準に3通り 5円を基準に2通り 10円を基準に1通
Incoming Term: 何通りあるか 数学,




0 件のコメント:
コメントを投稿