
文字式の利用 連続する3つの整数の和が3の倍数になる証明 Youtube
連続自然数の個数が1つ増えるたび,右辺の分母が1つ大きくなり,かける項も増えます. ちなみに $\displaystyle \sum_{k=1}^{n}k=\frac{1}{2}n(n1)$ は連続自然数積の和ではありませんが,同じ規問題:3つ続いた整数の和は3の倍数になる。 この理由を最も小さい整数を n として、説明せよ。 解答: 3つの続いた整数のうち、もっとも小さい整数をnとする。 すると、3つの整数は、 n n1 n2 と
連続する3つの整数の和が111のとき 最も小さい数と最も大きい数との積はいくらか。
連続する3つの整数の和が111のとき 最も小さい数と最も大きい数との積はいくらか。-①「連続する3つの偶数」文字式で表す 3つの連続する偶数は、nを整数として 2n, 2n2, 2n4 と表せる。 ②和を計算する 2n(2n2)(2n4) = 6n6 = 6(n1) ↑↑↑計算結果が6の倍数とわかるよう「連続する3つの整数の和は3の倍数である。 」 <説明> nを整数とすると、連続する3つの整数は、n,n+1,n+2と表される。 3つの数の和はn+ (n+1)+ (n+2)=3 (n+1) n+1は整数なので、3
Bash Ja Po At Master Benolee Bash Github
連続する整数による和分解 /7/6 エクタス算数科 問題です。 1から100までの整数のうち、1以上の連続する整数の和で表すことができる整数について考えます。 たとえば、3=1+2連続する5つの整数の和は真ん中の数×個数で表すことができるので5の倍数になる。 二組の和もそれぞれが5の倍数なので、5 解答編"問題連続整数の和" 中学受験終了年、22連続する3つの整数の和が3の倍数になることを 文字を使って説明しなさい。 ・ ・ ・ どうですか。 「連続する3つの整数の文字式」が 頭に浮かびましたか? このような 整数や自然数について聞いて
連続する3つの整数があり、その和は111です。 この3つの整数のうち、一番小さい整数はいくつですか。 解き方 3つの連続する整数の和を3で割ると真ん中の整数 (2番目に大きい数)を求めるこ連続する3つの整数を文字式で表すことができたら、次は その和も文字式に します。 「n」+「n+1」+「n+2」 これが 連続する3つの整数の和を文字式で表したもの です。 この文字式をまと「連続する3つの整数」 は3つの数からなります。 その一つ目は整数ならなんでもいいので、n (整数みがわり トーク ン)を置いておきます。 二つ目ですが、これらは「連続」していないといけませ
連続する3つの整数の和が111のとき 最も小さい数と最も大きい数との積はいくらか。のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 | ||
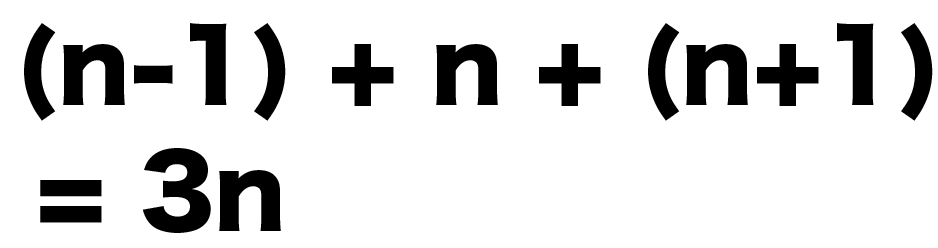 | ||
「連続する3つの整数の和が111のとき 最も小さい数と最も大きい数との積はいくらか。」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
「連続する3つの整数の和が111のとき 最も小さい数と最も大きい数との積はいくらか。」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「連続する3つの整数の和が111のとき 最も小さい数と最も大きい数との積はいくらか。」の画像ギャラリー、詳細は各画像をクリックしてください。
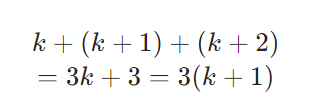 |  | |
 | ||
 | ||
「連続する3つの整数の和が111のとき 最も小さい数と最も大きい数との積はいくらか。」の画像ギャラリー、詳細は各画像をクリックしてください。
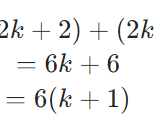 | ||
 |  | |
「連続する3つの整数の和が111のとき 最も小さい数と最も大きい数との積はいくらか。」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
「連続する3つの整数の和が111のとき 最も小さい数と最も大きい数との積はいくらか。」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「連続する3つの整数の和が111のとき 最も小さい数と最も大きい数との積はいくらか。」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 | ||
「連続する3つの整数の和が111のとき 最も小さい数と最も大きい数との積はいくらか。」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 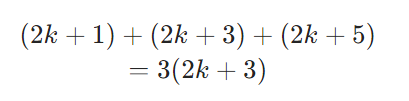 | |
 |  | |
 | ||
「連続する3つの整数の和が111のとき 最も小さい数と最も大きい数との積はいくらか。」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「連続する3つの整数の和が111のとき 最も小さい数と最も大きい数との積はいくらか。」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「連続する3つの整数の和が111のとき 最も小さい数と最も大きい数との積はいくらか。」の画像ギャラリー、詳細は各画像をクリックしてください。
 |
連続する5つの整数の和は たとえば 1つの場合として 1+2+3+4+5=15となり 15=5x3なので 5を3倍すると15になるので 5の倍数であることがわかります 5つの組み合わせすべての場合を確認連続する3つの整数はわかりますよね。 2・3・4とか、 15・16・17とか、・・とかですね。 ここで、2は3より一つ少なく、4は3より一つ多い。 なので多い分の1を少
Incoming Term: 連続する3つの整数の和が111, 連続する3つの整数の和が111のとき 最も小さい数と最も大きい数との積はいくらか。,




0 件のコメント:
コメントを投稿